Advertisements
Advertisements
Question
In the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 6, SQ = 8, PR = 15, find QR.
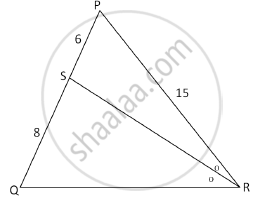
Solution
Seg RS bisects ∠PRQ ….(given)
`(PR)/(QR)= (PS)/(SQ)` ....(angle bisector property)
`15/(QR)=6/8`
`QR= (15xx8)/6=20`
RELATED QUESTIONS
In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC ∼ ΔPDB
(ii) PA.PB = PC.PD

State, true or false:
Two similar polygons are necessarily congruent.
In the given figure, ∆ABC and ∆AMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
- Prove that: ∆ABC ~ ∆AMP
- Find: AB and BC.

In the given figure, if ∠ADE = ∠B, show that ΔADE ~ ΔABC. If AD = 3.8cm, AE = 3.6cm, BE = 2.1cm and BC = 4.2cm, find DE.
D and E are points on the sides AB and AC respectively of Δ ABC such that AB=5.6cm, AD= 1.4cm, AC=7 .2cm and AE = 1.5 cm, show that DE is parallel to BC
In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find : If AP = x, then the value of AC in terms of x.

In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if:
- AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm.
- AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AE"/"EC"`
In ΔABC, BP and CQ are altitudes from B and C on AC and AB respectively. BP and CQ intersect at O. Prove that
(i) PC x OQ = QB x OP
(ii) `"OC"^2/"OB"^2 = ("PC" xx "PO")/("QB" xx "QO")`
AM and DN are the altitudes of two similar triangles ABC and DEF. Prove that: AM : DN = AB : DE.
PR = 26 cm, QR = 24 cm, ∠PAQ = 90°, PA = 6 cm and QA = 8 cm. Find ∠PQR
If ΔABC ~ ΔLMN and ∠B = 40°, then ∠M = ? Give reason.
In fig. BP ⊥ AC, CQ ⊥ AB, A−P−C, and A−Q−B then show that ΔAPB and ΔAQC are similar.
In ΔAPB and ΔAQC
∠APB = [ ]° ......(i)
∠AQC = [ ]° ......(ii)
∠APB ≅ ∠AQC .....[From (i) and (ii)]
∠PAB ≅ ∠QAC .....[______]
ΔAPB ~ ΔAQC .....[______]
There are two poles having heights 8 m and 4 m on plane ground as shown in fig. Because of sunlight shadows of smaller pole is 6m long, then find the length of shadow of longer pole.
In given fig., quadrilateral PQRS, side PQ || side SR, AR = 5 AP, then prove that, SR = 5PQ
It is given that ΔABC ~ ΔPQR, with `(BC)/(QR) = 1/3`. Then, `(ar(PRQ))/(ar(BCA))` is equal to ______.
If ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm and BC = 15 cm, then PR is equal to ______.
In the given figure, ΔABC ∼ ΔQPR, If AC = 6 cm, BC = 5 cm, QR = 3 cm and PR = x; them the value of x is ______.

In ΔPQR, S and T are points on PQ and PR respectively. `(PS)/(SQ) = (PT)/(TR)` and ∠PST = ∠PRQ. Prove that PQR is an isosceles triangle.
