Advertisements
Advertisements
Question
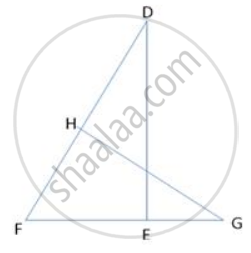
In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC ∼ ΔPDB
(ii) PA.PB = PC.PD
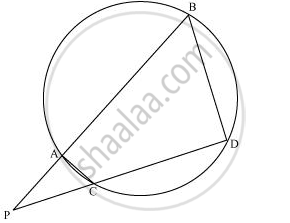
Solution
(i) In ΔPAC and ΔPDB,
∠P = ∠P (Common)
∠PAC = ∠PDB (Exterior angle of a cyclic quadrilateral is ∠PCA = ∠PBD equal to the opposite interior angle)
∴ ΔPAC ∼ ΔPDB
(ii)We know that the corresponding sides of similar triangles are proportional.
∴ PA/PD = AC/DB = PC/PB
=>PA/PD = PC/PB
∴ PA.PB = PC.PD
APPEARS IN
RELATED QUESTIONS
In figure, find ∠L
In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
In the following figure, DE || OQ and DF || OR, show that EF || QR.

ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that `("AO")/("BO") = ("CO")/("DO")`
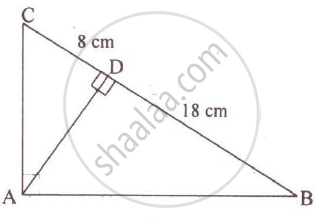
In the adjoining figure, ABC is a right angled triangle with ∠BAC = 90°.
1) Prove ΔADB ~ ΔCDA.
2) If BD = 18 cm CD = 8 cm Find AD.
3) Find the ratio of the area of ΔADB is to an area of ΔCDA.
Given: ∠GHE = ∠DFE = 90°,
DH = 8, DF = 12,
DG = 3x – 1 and DE = 4x + 2.
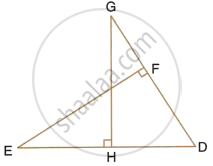
Find: the lengths of segments DG and DE.
Given: FB = FD, AE ⊥ FD and FC ⊥ AD.
Prove that: `(FB)/(AD) = (BC)/(ED)`.
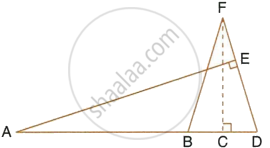
A vertical pole of length 7.5 cm casts a shadow 5 m long on the ground and at the same time a tower casts a shadow 24 m long. Find the height of the tower.
The corresponding altitudes of two similar triangles are 6cm and 9cm respectively. Find the ratio of their areas.
In the following figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and \[\text{AD} = 9 \text{ find} \frac{A\left( \Delta ABE \right)}{A\left( \Delta BAD \right)} \cdot\]
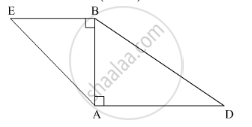
Select the appropriate alternative.
In ∆ABC and ∆PQR, in a one to one correspondence \[\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}\]
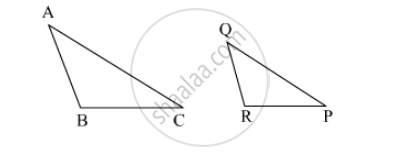
Prove that the area of Δ BCE described on one side BC of a square ABCD is one half the area of the similar Δ ACF described on the diagonal AC.
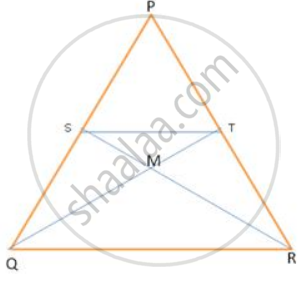
Figure shows Δ PQR in which ST || QR and SR and QT intersect each other at M. If `"PT"/"TR" = 5/3` find `("Ar" (triangle "MTS"))/("Ar" (triangle "MQR"))`
In figure , DEF is a right -angled triangle with ∠ E = 90 °.FE is produced to G and GH is drawn perpendicular to DE = 8 cm , DH = 8 cm ,DH = 6 cm and HF = 4 cm , find `("Ar" triangle "DEF")/("Ar" triangle "GHF")`
Δ ABC is similar to Δ PQR. If AB = 6cm, BC = 9cm, PQ = 9cm and PR = 10.5cm, find the lengths of AC and QR.
A ship is 400m laig and 100m wide. The length of its model is 20 cm. find the surface area of the deck of the model.
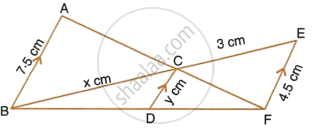
In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.
Points A(3, 1), B(5, 1), C(a, b) and D(4, 3) are vertices of a parallelogram ABCD. Find the values of a and b.
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
In the given figure ABC and CEF are two triangles where BA is parallel to CE and AF: AC = 5: 8.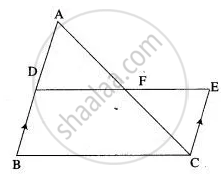
(i) Prove that ΔADF ∼ ΔCEF
(ii) Find AD if CE = 6 cm
(iii) If DF is parallel to BC find area of ΔADF: area of ΔABC.
In figure, PQ is parallel to BC, AP : AB = 2 : 7. If QC = 0 and BC = 21,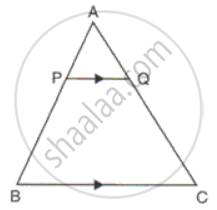
Find
(i) AQ
(ii) PQ
A girl looks the reflection of the top of the lamp post on the mirror which is 6.6 m away from the foot of the lamppost. The girl whose height is 1.25 m is standing 2.5 m away from the mirror. Assuming the mirror is placed on the ground facing the sky and the girl, mirror and the lamppost are in the same line, find the height of the lamp post.
In ∆LMN, ∠L = 60°, ∠M = 50°. If ∆LMN ~ ∆PQR then the value of ∠R is
PR = 26 cm, QR = 24 cm, ∠PAQ = 90°, PA = 6 cm and QA = 8 cm. Find ∠PQR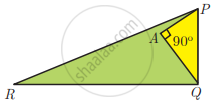
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 = `"p"^2 + "a"x + "a"^2/4`
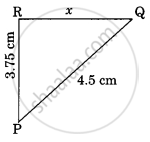
In the given figure ΔABC ~ ΔPQR. The value of x is
 |
 |
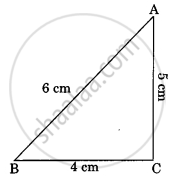
In the given figure, ∠ACB = ∠CDA, AC = 8cm, AD = 3cm, then BD is ______.
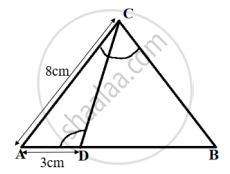
ABCD is a parallelogram. Point P divides AB in the ratio 2:3 and point Q divides DC in the ratio 4:1. Prove that OC is half of OA.

