Advertisements
Advertisements
Question
The corresponding altitudes of two similar triangles are 6cm and 9cm respectively. Find the ratio of their areas.
Solution
Let the two triangles be ABC and DEF with altitudes AP and DQ, respectively.
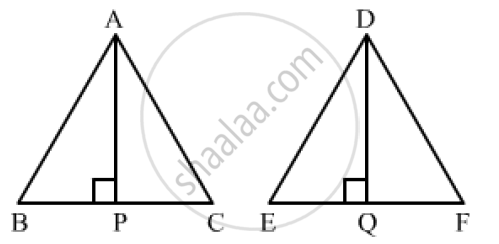
It is given that Δ ABC ~ Δ DEF.
We know that the ration of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
`(ar(ΔABC))/(ar(ΔDEF))=(AP)^2/(DQ)^2`
⇒ `(ar(ΔABC))/(ar(ΔDEF))=6^2/9^2`
=`36/81`
=`4/9`
Hence, the ratio of their areas is 4 : 9
APPEARS IN
RELATED QUESTIONS
In figure, ∠CAB = 90º and AD ⊥ BC. If AC = 75 cm, AB = 1 m and BD = 1.25 m, find AD.
P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm, PB = 6cm. AQ = 5 cm and QC = 10 cm, show that BC = 3PQ.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that `("AO")/("BO") = ("CO")/("DO")`
In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC ∼ ΔPDB
(ii) PA.PB = PC.PD

State, true or false:
Two similar polygons are necessarily congruent.
Given: ∠GHE = ∠DFE = 90°,
DH = 8, DF = 12,
DG = 3x – 1 and DE = 4x + 2.

Find: the lengths of segments DG and DE.
Area of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
The given diagram shows two isosceles triangles which are similar. In the given diagram, PQ and BC are not parallel; PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ.

Calculate:
- the length of AP,
- the ratio of the areas of triangle APQ and triangle ABC.
In the given figure, triangle ABC is similar to triangle PQR. AM and PN are altitudes whereas AX and PY are medians.
prove that
`("AM")/("PN")=("AX")/("PY")`
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In the given figure, ∠ABC = 90° and BD⊥AC. If BD = 8cm, AD = 4cm, find CD.
In the given figure, ∠1 = ∠2 and `(AC)/(BD)=(CB)/(CE)` Prove that Δ ACB ~ Δ DCE.
In the given figure, seg XY || seg BC, then which of the following statements is true?

Δ ABC ~ Δ DEF. If BC = 3cm , EF=4cm and area of Δ ABC = 54 cm2 , find area of Δ DEF.
In Δ ABC , MN || BC .

If BC = 14 cm and MN = 6 cm , find `("Ar" triangle "AMN")/("Ar" . ("trapezium MBCN"))`
In Δ ABC, D and E are points on the sides AB and AC respectively. If AD= 4cm, DB=4.Scm, AE=6.4cm and EC=7.2cm, find if DE is parallel to BC or not.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The area in km2 that can be represented by 1 cm2
A line segment DE is drawn parallel to base BC of ΔABC which cuts AB at point D and AC at point E. If AB = 5BD and EC = 3.2 cm, find the length of AE.
In the figure, given below, PQR is a right-angle triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.

The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.

Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are `3/5` of the corresponding sides of the first triangle.
D and E are points on the sides AB and AC respectively of a Δ ABC such that DE | | BC and divides Δ ABC into two parts, equal in area. Find `"BD"/"AB"`.
Through the vertex S of a parallelogram PQRS, a line is drawn to intersect the sides Qp and QR produced at M and N respectively. Prove that `"SP"/"PM" = "MQ"/"QN" = "MR"/"SR"`
A model of a ship is made to a scale of 1:500. Find: The volume of the model when the volume of the ship is 1km3
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The area of the plot in sq km
Construct a triangle similar to a given triangle PQR with its sides equal to `2/3` of the corresponding sides of the triangle PQR (scale factor `2/3 < 1`)
In the given figure, UB || AT and CU ≡ CB Prove that ΔCUB ~ ΔCAT and hence ΔCAT is isosceles.
In fig. BP ⊥ AC, CQ ⊥ AB, A−P−C, and A−Q−B then show that ΔAPB and ΔAQC are similar.
In ΔAPB and ΔAQC
∠APB = [ ]° ......(i)
∠AQC = [ ]° ......(ii)
∠APB ≅ ∠AQC .....[From (i) and (ii)]
∠PAB ≅ ∠QAC .....[______]
ΔAPB ~ ΔAQC .....[______]
In fig., seg AC and seg BD intersect each other at point P.

`"AP"/"PC" = "BP"/"PD"` then prove that ΔABP ~ ΔCDP
ΔABP ~ ΔDEF and A(ΔABP) : A(ΔDEF) = 144:81, then AB : DE = ?
