Advertisements
Advertisements
Question
The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.

Solution
AF = 8 cm and AB = 12cm
So, FB = 20 cm
In ΔDEC and ΔEAF
∠DEC = ∠EAF ...(Vertically opposite angles)
∠EDC = ∠EAF ...(Alternate angles)
So, ΔDEC ∼ ΔAEF ...(AA criterion for similarity)
`=> (DE)/(AE) = (EC)/(EF) = (DC)/(AF)`
`=> (DE)/(AE) = (DC)/(AF)`
`=> (DE)/(AE) = (AB)/(AF)`
`=> (DE)/4 = 12/8`
`=>` DE = 6 cm
So, AD = AE + ED
= 4 + 6
= 10 cm
Perimeter of the parallelogram ABCD
= AB + BC + CD + AD
= 12 + 10 + 12 + 10
= 44 cm
Notes
Δ
APPEARS IN
RELATED QUESTIONS
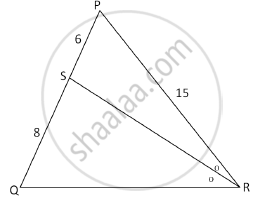
In the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 6, SQ = 8, PR = 15, find QR.
P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm, PB = 6cm. AQ = 5 cm and QC = 10 cm, show that BC = 3PQ.
ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.
In the following figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and \[\text{AD} = 9 \text{ find} \frac{A\left( \Delta ABE \right)}{A\left( \Delta BAD \right)} \cdot\]


O is any point in the interior of ΔABC. Bisectors of ∠AOB, ∠BOC and ∠AOC intersect side AB, side BC, side AC in
F, D and E respectively.
Prove that
BF × AE × CD = AF × CE × BD
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OC', if OC = 21 cm.
Also, state the value of :
- `(OB^')/(OB)`
- `(C^'A^')/(CA)`
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AE"/"AC"`
In ΔABC, BP and CQ are altitudes from B and C on AC and AB respectively. BP and CQ intersect at O. Prove that
(i) PC x OQ = QB x OP
(ii) `"OC"^2/"OB"^2 = ("PC" xx "PO")/("QB" xx "QO")`
Find the scale factor in each of the following and state the type of size transformation:
Image length = 8cm, Actual length = 20cm.
If in triangles ABC and EDF, `"AB"/"DE" = "BC"/"FD"` then they will be similar, when
