Advertisements
Advertisements
Question
ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.
Solution
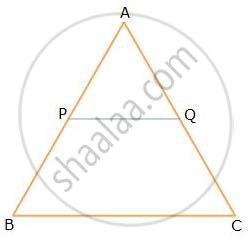
From the given information, we have:
`ar (∆APQ) = 1/2 ar(∆ABC)`
`=> (ar(ΔAPQ))/(ar(ΔABC)) = 1/2`
`=> (AP^2)/(AB^2) = 1/2`
`=> (AP)/(AB) = 1/sqrt(2)`
`=> (AB - BP)/(AB) = 1/sqrt(2)`
`=> 1 - (BP)/(AB) = 1/sqrt(2)`
`=> (BP)/(AB) = 1 - 1/sqrt(2)`
`=> (BP)/(AB) = (sqrt(2) - 1)/sqrt(2) = (2 - sqrt(2))/2`
APPEARS IN
RELATED QUESTIONS
The perimeter of two similar triangles are 30 cm and 24 cm. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the midpoints of AB, AC, CD and BD respectively, show that PQRS is a rhombus.

In ΔABC, D and E are the midpoints of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.

In ΔPQR, PQ = 10 cm, QR = 12cm, PR = 8 cm, find the biggest and the smallest angle of the triangle.
AD and BC are two straight lines intersecting at 0. CD and BA are perpendirulars from Band Con AD. If AB=6cm, CD =9cm, AD =20cm and BC=25cm, find the lengths of AO, BO, CO and DO.
In ΔABC, DE is drawn parallel to BC cutting AB in the ratio 2 : 3. Calculate:
(i) `("area"(Δ"ADE"))/("area"(Δ"ABC")`
(i) `("area"("trapeziumEDBC"))/("area"(Δ"ABC"))`
If ∆ABC ~ ∆DEF such that area of ∆ABC is 9 cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
PR = 26 cm, QR = 24 cm, ∠PAQ = 90°, PA = 6 cm and QA = 8 cm. Find ∠PQR
In the given figure AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.
In a square of side 10 cm, its diagonal = ______.
