Advertisements
Advertisements
Question
In the given triangle PQR, LM is parallel to QR and PM : MR = 3 : 4.
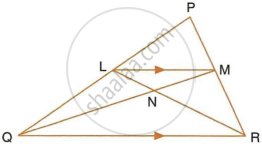
Calculate the value of ratio:
- `(PL)/(PQ)` and then `(LM)/(QR)`
- `"Area of ΔLMN"/"Area of ΔMNR"`
- `"Area of ΔLQM"/"Area of ΔLQN"`
Solution
i. In ∆PLM and ∆PQR,
As LM || QR, Corresponding angles are equal
∠PLM = ∠PQR
∠PML = ∠PRQ
∆PLM ~ ∆PQR
`=> 3/7 = (LM)/(QR)` ...`(∵ (PM)/(MR) = 3/4 => (PM)/(PR) = 3/7)`
Also, by using basic proportionality theorem, we have:
`(PL)/(LQ) = (PM)/(MR) = 3/4`
`=> (LQ)/(PL) = 4/3`
`=> 1 + (LQ)/(PL) = 1 + 4/3`
`=> (PL + LQ)/(PL) = (3 + 4)/3`
`=> (PQ)/(PL) = 7/3`
`=> (PL)/(PQ) = 3/7`
ii. Since ∆LMN and ∆MNR have common vertex at M and their bases LN and NR are along the same straight line
∴ `"Area of ΔLMN"/"Area of ΔMNR" = (LN)/(NR)`
Now, in ∆LNM and ∆RNQ
∠NLM = ∠NRQ ...(Alternate angles)
∠LMN = ∠NQR ...(Alternate angles)
∆LMN ~ ∆RNQ ...(AA Similarity)
∴ `(MN)/(QN) = (LN)/(NR) = (LM)/(QR) = 3/7`
∴ `"Area of ΔLMN"/"Area of ΔMNR" = (LN)/(NR) = 3/7`
iii. Since ΔLQM and ΔLQN have common vertex at L and their bases QM and QN are along the same straight line
`"Area of ΔLQM"/ "Area of ΔLQN" = (QM)/(QN) = 10/7`
`(∴ (NM)/(QN) = 3/7 => (QM)/(QN) = 10/7)`
APPEARS IN
RELATED QUESTIONS
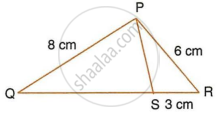
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
- Prove ΔPQR ∼ ΔSPR.
- Find the length of QR and PS.
- `"area of ΔPQR"/"area of ΔSPR"`
Given: RS and PT are altitudes of ΔPQR. Prove that:
- ΔPQT ~ ΔQRS,
- PQ × QS = RQ × QT.
In ∆PQR, ∠Q = 90° and QM is perpendicular to PR. Prove that:
- PQ2 = PM × PR
- QR2 = PR × MR
- PQ2 + QR2 = PR2
In the right-angled triangle QPR, PM is an altitude.
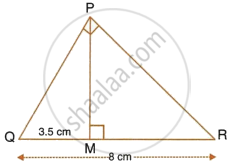
Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.
In the given figure, AX : XB = 3 : 5
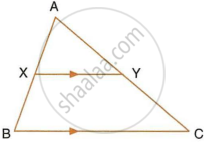
Find:
- the length of BC, if the length of XY is 18 cm.
- the ratio between the areas of trapezium XBCY and triangle ABC.
In the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.
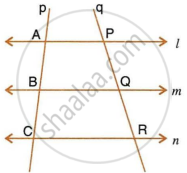
Prove that : `(AB)/(BC) = (PQ)/(QR)`
In the given figure, triangle ABC is similar to triangle PQR. AM and PN are altitudes whereas AX and PY are medians.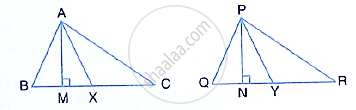
Prove that : `(AM)/(PN)=(AX)/(PY)`
The dimensions of the model of a multistoreyed building are 1 m by 60 cm by 1.20 m. If the scale factor is 1 : 50, find the actual dimensions of the building.
Also, find:
- the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq. cm.
- the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m3.
In the give figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that ΔABC ∼ ΔEBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the:
- length of AB
- area of ΔABC
In fig. ABCD is a trapezium in which AB | | DC and AB = 2DC. Determine the ratio between the areas of ΔAOB and ΔCOD.
