Advertisements
Advertisements
प्रश्न
In the given triangle PQR, LM is parallel to QR and PM : MR = 3 : 4.
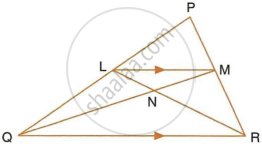
Calculate the value of ratio:
- `(PL)/(PQ)` and then `(LM)/(QR)`
- `"Area of ΔLMN"/"Area of ΔMNR"`
- `"Area of ΔLQM"/"Area of ΔLQN"`
उत्तर
i. In ∆PLM and ∆PQR,
As LM || QR, Corresponding angles are equal
∠PLM = ∠PQR
∠PML = ∠PRQ
∆PLM ~ ∆PQR
`=> 3/7 = (LM)/(QR)` ...`(∵ (PM)/(MR) = 3/4 => (PM)/(PR) = 3/7)`
Also, by using basic proportionality theorem, we have:
`(PL)/(LQ) = (PM)/(MR) = 3/4`
`=> (LQ)/(PL) = 4/3`
`=> 1 + (LQ)/(PL) = 1 + 4/3`
`=> (PL + LQ)/(PL) = (3 + 4)/3`
`=> (PQ)/(PL) = 7/3`
`=> (PL)/(PQ) = 3/7`
ii. Since ∆LMN and ∆MNR have common vertex at M and their bases LN and NR are along the same straight line
∴ `"Area of ΔLMN"/"Area of ΔMNR" = (LN)/(NR)`
Now, in ∆LNM and ∆RNQ
∠NLM = ∠NRQ ...(Alternate angles)
∠LMN = ∠NQR ...(Alternate angles)
∆LMN ~ ∆RNQ ...(AA Similarity)
∴ `(MN)/(QN) = (LN)/(NR) = (LM)/(QR) = 3/7`
∴ `"Area of ΔLMN"/"Area of ΔMNR" = (LN)/(NR) = 3/7`
iii. Since ΔLQM and ΔLQN have common vertex at L and their bases QM and QN are along the same straight line
`"Area of ΔLQM"/ "Area of ΔLQN" = (QM)/(QN) = 10/7`
`(∴ (NM)/(QN) = 3/7 => (QM)/(QN) = 10/7)`
APPEARS IN
संबंधित प्रश्न
Given: RS and PT are altitudes of ΔPQR. Prove that:
- ΔPQT ~ ΔQRS,
- PQ × QS = RQ × QT.
Given: ABCD is a rhombus, DPR and CBR are straight lines.
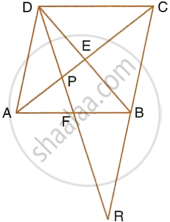
Prove that: DP × CR = DC × PR.
In ∆ABC, right – angled at C, CD ⊥ AB.
Prove:
`"CD"^2 = "AD"xx "DB"`
In the given figure, P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC.
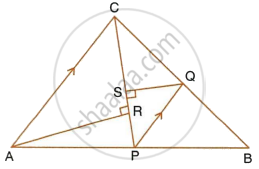
- Calculate the ratio PQ : AC, giving reason for your answer.
- In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°. Given QS = 6 cm, calculate the length of AR.
In the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.
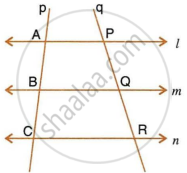
Prove that : `(AB)/(BC) = (PQ)/(QR)`
In the given figure, triangle ABC is similar to triangle PQR. AM and PN are altitudes whereas AX and PY are medians.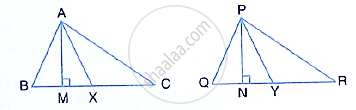 Prove that : `(AM)/(PN)=(AX)/(PY)`
Prove that : `(AM)/(PN)=(AX)/(PY)`
The dimensions of the model of a multistoreyed building are 1 m by 60 cm by 1.20 m. If the scale factor is 1 : 50, find the actual dimensions of the building.
Also, find:
- the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq. cm.
- the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m3.
A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to ΔDEF such that the longest side of ΔDEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of ΔDEF.
Two isosceles triangles have equal vertical angles. Show that the triangles are similar. If the ratio between the areas of these two triangles is 16 : 25, find the ratio between their corresponding altitudes.
The following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively.
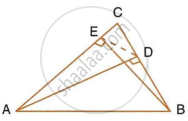
Show that:
- ΔADC ∼ ΔBEC
- CA × CE = CB × CD
- ΔABC ~ ΔDEC
- CD × AB = CA × DE
