Advertisements
Advertisements
प्रश्न
Given: RS and PT are altitudes of ΔPQR. Prove that:
- ΔPQT ~ ΔQRS,
- PQ × QS = RQ × QT.
उत्तर
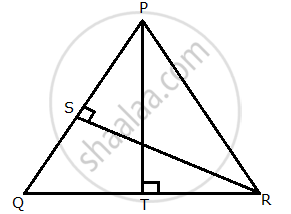
i.
In ∆PQT and ∆QRS,
∠PTQ = ∠RSQ = 90° ...(Given)
∠PQT = ∠RQS ...(Common)
∆PQT ~ ∆RQS ...(By AA similarity)
ii.
Since, triangle PQT and RQS are similar
∴ `(PQ)/(RQ) = (QT)/(QS)`
`=>` PQ × QS = RQ × QT
APPEARS IN
संबंधित प्रश्न
In ∆PQR, ∠Q = 90° and QM is perpendicular to PR. Prove that:
- PQ2 = PM × PR
- QR2 = PR × MR
- PQ2 + QR2 = PR2
In ∆ABC, ∠B = 90° and BD ⊥ AC.
- If CD = 10 cm and BD = 8 cm; find AD.
- If AC = 18 cm and AD = 6 cm; find BD.
- If AC = 9 cm and AB = 7 cm; find AD.
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produces at Q. Given the area of triangle CPQ = 20 cm2.
Calculate:
- area of triangle CDP,
- area of parallelogram ABCD.
In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ∆ABC and ∆DEC.
An aeroplane is 30 m long and its model is 15 cm long. If the total outer surface area of the model is 150 cm2, find the cost of painting the outer surface of the aeroplane at the rate of Rs.120 per sq. m. Given that 50 sq. m of the surface of the aeroplane is left for windows.
In the given figure, triangle ABC is similar to triangle PQR. AM and PN are altitudes whereas AX and PY are medians.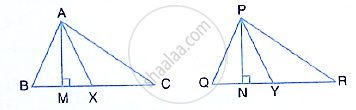
Prove that : `(AM)/(PN)=(AX)/(PY)`
The ratio between the altitudes of two similar triangles is 3 : 5; write the ratio between their :
- corresponding medians.
- perimeters.
- areas.
On a map, drawn to a scale of 1 : 20000, a rectangular plot of land ABCD has AB = 24 cm and BC = 32 cm. Calculate :
- the diagonal distance of the plot in kilometer.
- the area of the plot in sq. km.
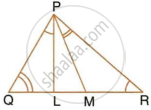
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that:
- ΔPQL ∼ ΔRPM
- QL × RM = PL × PM
- PQ2 = QR × QL
A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to ΔDEF such that the longest side of ΔDEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of ΔDEF.
