Advertisements
Advertisements
प्रश्न
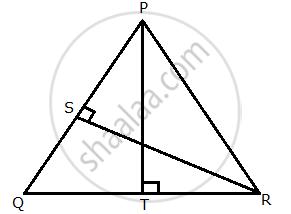
Given: RS and PT are altitudes of ΔPQR. Prove that:
- ΔPQT ~ ΔQRS,
- PQ × QS = RQ × QT.
उत्तर
i.
In ∆PQT and ∆QRS,
∠PTQ = ∠RSQ = 90° ...(Given)
∠PQT = ∠RQS ...(Common)
∆PQT ~ ∆RQS ...(By AA similarity)
ii.
Since, triangle PQT and RQS are similar
∴ `(PQ)/(RQ) = (QT)/(QS)`
`=>` PQ × QS = RQ × QT
APPEARS IN
संबंधित प्रश्न
In ∆ABC, right – angled at C, CD ⊥ AB.
Prove:
`"CD"^2 = "AD"xx "DB"`
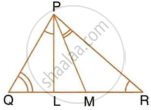
In the right-angled triangle QPR, PM is an altitude.
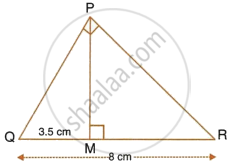
Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.
In the given figure, AX : XB = 3 : 5
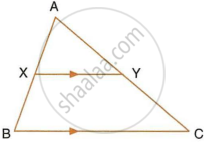
Find:
- the length of BC, if the length of XY is 18 cm.
- the ratio between the areas of trapezium XBCY and triangle ABC.
In the given triangle PQR, LM is parallel to QR and PM : MR = 3 : 4.
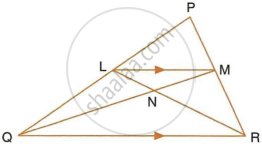
Calculate the value of ratio:
- `(PL)/(PQ)` and then `(LM)/(QR)`
- `"Area of ΔLMN"/"Area of ΔMNR"`
- `"Area of ΔLQM"/"Area of ΔLQN"`
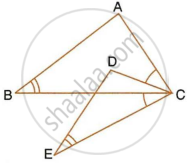
In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ∆ABC and ∆DEC.
The ratio between the areas of two similar triangles is 16 : 25. State the ratio between their :
- perimeters.
- corresponding altitudes.
- corresponding medians.
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that:
- ΔPQL ∼ ΔRPM
- QL × RM = PL × PM
- PQ2 = QR × QL
Two isosceles triangles have equal vertical angles. Show that the triangles are similar. If the ratio between the areas of these two triangles is 16 : 25, find the ratio between their corresponding altitudes.
The following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively.
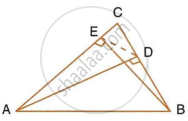
Show that:
- ΔADC ∼ ΔBEC
- CA × CE = CB × CD
- ΔABC ~ ΔDEC
- CD × AB = CA × DE
In fig. ABCD is a trapezium in which AB | | DC and AB = 2DC. Determine the ratio between the areas of ΔAOB and ΔCOD.