Advertisements
Advertisements
प्रश्न
In fig. ABCD is a trapezium in which AB | | DC and AB = 2DC. Determine the ratio between the areas of ΔAOB and ΔCOD.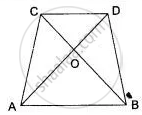
उत्तर
In triangle AOB and COD, we have
∠AOB = ∠COD, ...[Vertically opposite angles]
and ∠OAB = ∠OCD, ...[Corresponding angles]
So, by AA-criterion of similarly, we have
ΔAOB ∼ ΔCOD
⇒ `"Area (ΔAOB)"/"Area (ΔCOD)" = "AB"^2/"DC"^2`
⇒ `"Area (ΔAOB)"/"Area (ΔCOD)" = (2"DC")^2/("DC")^2`
= `(4)/(1)`
Hence, area (ΔAOB) : area(ΔCOD) = 4 : 1.
APPEARS IN
संबंधित प्रश्न
Given: RS and PT are altitudes of ΔPQR. Prove that:
- ΔPQT ~ ΔQRS,
- PQ × QS = RQ × QT.
Given: ABCD is a rhombus, DPR and CBR are straight lines.
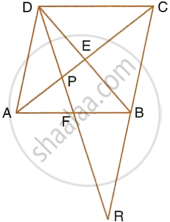
Prove that: DP × CR = DC × PR.
In ∆PQR, ∠Q = 90° and QM is perpendicular to PR. Prove that:
- PQ2 = PM × PR
- QR2 = PR × MR
- PQ2 + QR2 = PR2
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produces at Q. Given the area of triangle CPQ = 20 cm2.

Calculate:
- area of triangle CDP,
- area of parallelogram ABCD.
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB)=3/2`
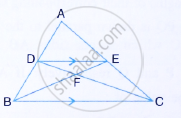
(1) Determine the ratios `(AD)/(AB) and (DE)/(BC)`
(2 ) Prove that ∆DEF is similar to ∆CBF Hence, find `(EF)/(FB)`.
(3) What is the ratio of the areas of ∆DEF and ∆BFC.
In the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.
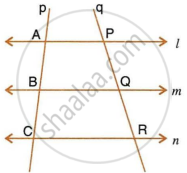
Prove that : `(AB)/(BC) = (PQ)/(QR)`
The ratio between the altitudes of two similar triangles is 3 : 5; write the ratio between their :
- corresponding medians.
- perimeters.
- areas.
The ratio between the areas of two similar triangles is 16 : 25. State the ratio between their :
- perimeters.
- corresponding altitudes.
- corresponding medians.
In the give figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that ΔABC ∼ ΔEBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the:
- length of AB
- area of ΔABC

