Advertisements
Advertisements
प्रश्न
In the give figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that ΔABC ∼ ΔEBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the:
- length of AB
- area of ΔABC

उत्तर
In ΔABC and ΔEBD
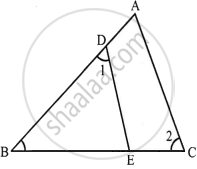
∠1 = ∠2 ...(Given)
∠B = ∠B ...(Common)
`\implies` ΔABC ∼ ΔEBD ...[By AA axiom of similarity]
Now, `"Area of ΔABC"/"Area of ΔEBD" = ((BC)/(BD))^2`
`\implies "Area of ΔABC"/9 = (10/5)^2`
`\implies` Area of ΔABC = 4 × 9
`\implies` Area of ΔABC = 36 cm2
Also, `"Area of ΔABC"/"Area of ΔEBD" = (AB)^2/(BE)^2`
`\implies 36/9 = (AB^2)/36`
`\implies AB^2 = (36 xx 36)/9`
`\implies` AB2 = 144
`\implies` AB = 12 cm
APPEARS IN
संबंधित प्रश्न
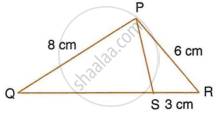
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
- Prove ΔPQR ∼ ΔSPR.
- Find the length of QR and PS.
- `"area of ΔPQR"/"area of ΔSPR"`
In ∆ ABC, ∠B = 2 ∠C and the bisector of angle B meets CA at point D. Prove that:
(i) ∆ ABC and ∆ ABD are similar,
(ii) DC: AD = BC: AB
Given : AB || DE and BC || EF. Prove that :
- `(AD)/(DG) = (CF)/(FG)`
- ∆DFG ∼ ∆ACG
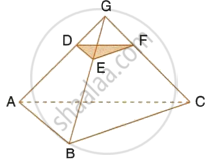
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produces at Q. Given the area of triangle CPQ = 20 cm2.

Calculate:
- area of triangle CDP,
- area of parallelogram ABCD.
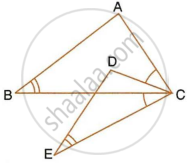
In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ∆ABC and ∆DEC.
Triangle ABC is an isosceles triangle in which AB = AC = 13 cm and BC = 10 cm. AD is
perpendicular to BC. If CE = 8 cm and EF ⊥ AB, find:
i)`"area of ADC"/"area of FEB"` ii)`"area of ΔAFEB"/"area of ΔABC"`

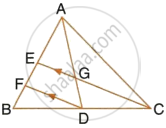
In the following figure, AD and CE are medians of ΔABC. DF is drawn parallel to CE. Prove that :
- EF = FB,
- AG : GD = 2 : 1
The dimensions of the model of a multistoreyed building are 1 m by 60 cm by 1.20 m. If the scale factor is 1 : 50, find the actual dimensions of the building.
Also, find:
- the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq. cm.
- the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m3.
The following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively.
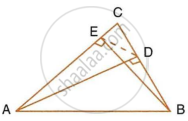
Show that:
- ΔADC ∼ ΔBEC
- CA × CE = CB × CD
- ΔABC ~ ΔDEC
- CD × AB = CA × DE
