Advertisements
Advertisements
प्रश्न
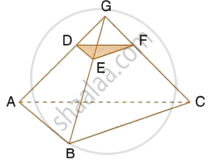
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
उत्तर
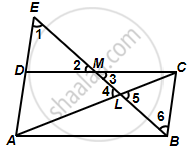
∠1 = ∠6 ...(Alternate interior angles)
∠2 = ∠3 ...(Vertically opposite angles)
DM = MC ...(M is the mid-point of CD)
∴ ∆DEM ≅ ∆CBM ...(AAS congruence criterion)
So, DE = BC ...(Corresponding parts of congruent triangles)
Also, AD = BC ...(Opposite sides of a parallelogram)
`=>` AE = AD + DE = 2BC
Now, ∠1 = ∠6 and ∠4 = ∠5
∴ ∆ELA ~ ∆BLC ...(AA similarity)
`=> (EL)/(BL) = (EA)/(BC)`
`=> (EL)/(BL) = (2BC)/(BC) = 2`
`=>` EL = 2BL
संबंधित प्रश्न
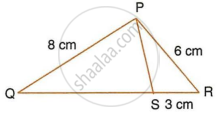
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
- Prove ΔPQR ∼ ΔSPR.
- Find the length of QR and PS.
- `"area of ΔPQR"/"area of ΔSPR"`
Given: RS and PT are altitudes of ΔPQR. Prove that:
- ΔPQT ~ ΔQRS,
- PQ × QS = RQ × QT.
Given: ABCD is a rhombus, DPR and CBR are straight lines.
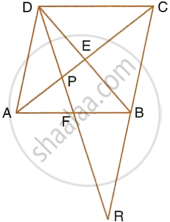
Prove that: DP × CR = DC × PR.
Given : AB || DE and BC || EF. Prove that :
- `(AD)/(DG) = (CF)/(FG)`
- ∆DFG ∼ ∆ACG
In the right-angled triangle QPR, PM is an altitude.
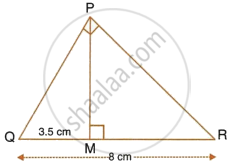
Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.
In the given triangle PQR, LM is parallel to QR and PM : MR = 3 : 4.
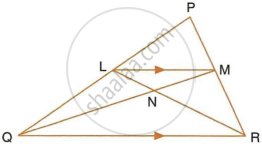
Calculate the value of ratio:
- `(PL)/(PQ)` and then `(LM)/(QR)`
- `"Area of ΔLMN"/"Area of ΔMNR"`
- `"Area of ΔLQM"/"Area of ΔLQN"`
In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ∆ABC and ∆DEC.
In the following figure, AB, CD and EF are parallel lines. AB = 6cm, CD = y cm, EF = 10 cm, AC = 4 cm and CF = x cm. Calculate x and y 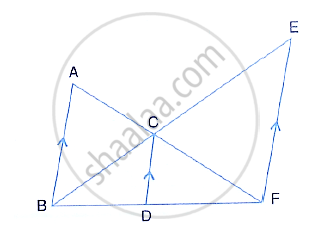
In the give figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that ΔABC ∼ ΔEBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the:
- length of AB
- area of ΔABC

In fig. ABCD is a trapezium in which AB | | DC and AB = 2DC. Determine the ratio between the areas of ΔAOB and ΔCOD.