Advertisements
Advertisements
प्रश्न
Given: ABCD is a rhombus, DPR and CBR are straight lines.
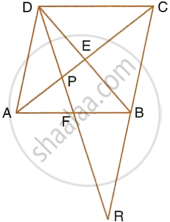
Prove that: DP × CR = DC × PR.
उत्तर
In ∆DPA and ∆RPC,
∠DPA = ∠RPC ...(Vertically opposite angles)
∠PAD = ∠PCR ...(Alternate angles)
∆DPA ~ ∆RPC
∴ `(DP)/(PR) = (AD)/(CR)`
`(DP)/(PR) = (DC)/(CR)` ...(AD = DC, as ABCD is rhombus)
Hence, DP × CR = DC × PR
APPEARS IN
संबंधित प्रश्न
In ∆ABC, right – angled at C, CD ⊥ AB.
Prove:
`"CD"^2 = "AD"xx "DB"`
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the given figure, P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC.
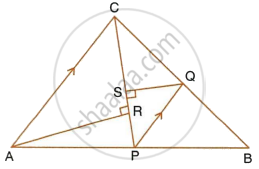
- Calculate the ratio PQ : AC, giving reason for your answer.
- In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°. Given QS = 6 cm, calculate the length of AR.
In the right-angled triangle QPR, PM is an altitude.
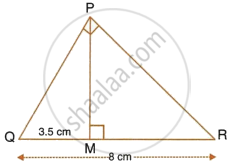
Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.
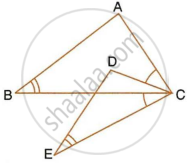
In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ∆ABC and ∆DEC.
Triangle ABC is an isosceles triangle in which AB = AC = 13 cm and BC = 10 cm. AD is
perpendicular to BC. If CE = 8 cm and EF ⊥ AB, find:
i)`"area of ADC"/"area of FEB"` ii)`"area of ΔAFEB"/"area of ΔABC"`

The ratio between the altitudes of two similar triangles is 3 : 5; write the ratio between their :
- corresponding medians.
- perimeters.
- areas.
In ΔABC, ∠ACB = 90° and CD ⊥ AB.
Prove that : `(BC^2)/(AC^2)=(BD)/(AD)`
A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to ΔDEF such that the longest side of ΔDEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of ΔDEF.
The following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively.
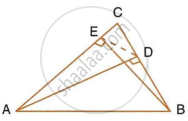
Show that:
- ΔADC ∼ ΔBEC
- CA × CE = CB × CD
- ΔABC ~ ΔDEC
- CD × AB = CA × DE
