Advertisements
Advertisements
प्रश्न
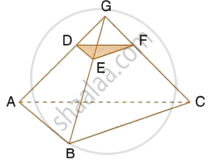
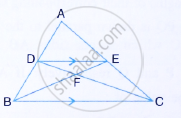
Given : AB || DE and BC || EF. Prove that :
- `(AD)/(DG) = (CF)/(FG)`
- ∆DFG ∼ ∆ACG
उत्तर
i. In ΔAGB, DE || AB, by Basic proportionality theorem
`(GD)/(DA) = (GE)/(EB)` ...(1)
In ΔGBC, EF || BC, by Basic proportionality theorem,
`(GE)/(EB) = (GF)/(FC)` ...(2)
From (1) and (2), we get
`(GD)/(DA) = (GF)/(FC)`
`(AD)/(DG) = (CF)/(FG)`
ii.
From (i), we have:
`(AD)/(DG) = (CF)/(FG)`
∠DGF = ∠AGC ...(Common)
∴ ΔDFG ∼ ΔACG ...(SAS similarity)
APPEARS IN
संबंधित प्रश्न
Given: ABCD is a rhombus, DPR and CBR are straight lines.
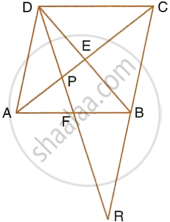
Prove that: DP × CR = DC × PR.
In ∆ABC, right – angled at C, CD ⊥ AB.
Prove:
`"CD"^2 = "AD"xx "DB"`
In the right-angled triangle QPR, PM is an altitude.
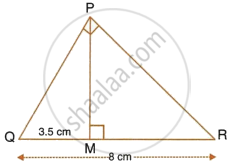
Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.
In the given figure, AX : XB = 3 : 5
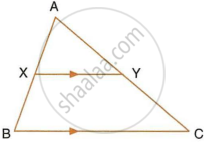
Find:
- the length of BC, if the length of XY is 18 cm.
- the ratio between the areas of trapezium XBCY and triangle ABC.
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produces at Q. Given the area of triangle CPQ = 20 cm2.
Calculate:
- area of triangle CDP,
- area of parallelogram ABCD.
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB)=3/2`
(1) Determine the ratios `(AD)/(AB) and (DE)/(BC)`
(2 ) Prove that ∆DEF is similar to ∆CBF Hence, find `(EF)/(FB)`.
(3) What is the ratio of the areas of ∆DEF and ∆BFC.
In the given figure, triangle ABC is similar to triangle PQR. AM and PN are altitudes whereas AX and PY are medians.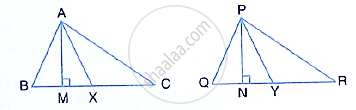
Prove that : `(AM)/(PN)=(AX)/(PY)`
In ΔABC, ∠ACB = 90° and CD ⊥ AB.
Prove that : `(BC^2)/(AC^2)=(BD)/(AD)`
In triangle ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA.
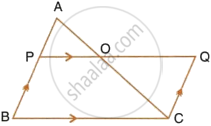
Find:
- area ΔAPO : area ΔABC.
- area ΔAPO : area ΔCQO.
In the give figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that ΔABC ∼ ΔEBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the:
- length of AB
- area of ΔABC
