Advertisements
Advertisements
प्रश्न
In the given figure, AX : XB = 3 : 5
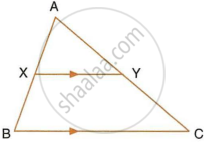
Find:
- the length of BC, if the length of XY is 18 cm.
- the ratio between the areas of trapezium XBCY and triangle ABC.
उत्तर
Given,
`(AX)/(XB) = 3/5 => (AX)/(AB) = 3/8` ...(1)
i. In ΔAXY and ΔABC,
As XY || BC, Corresponding angles are equal
∠AXY = ∠ABC
∠AYX = ∠ACB
ΔAXY ~ ΔABC
`=> (AX)/(AB) = (XY)/(BC)`
`=> 3/8 = 18/(BC)`
`=>` BC = 48 cm
ii. `"Area of ΔAXY"/"Area of ΔABC" = (AX^2)/(AB^2) = 9/64`
`"Area of ΔABC – Area of ΔAXY"/"Area of ΔABC" = (64 - 9)/64 = 55/64`
`"Area of trapezium XBCY"/"Area of ΔABC" = 55/64`
APPEARS IN
संबंधित प्रश्न
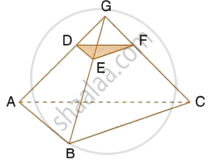
Given : AB || DE and BC || EF. Prove that :
- `(AD)/(DG) = (CF)/(FG)`
- ∆DFG ∼ ∆ACG
In the right-angled triangle QPR, PM is an altitude.
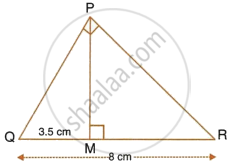
Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB)=3/2`
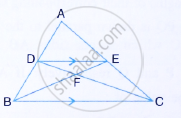
(1) Determine the ratios `(AD)/(AB) and (DE)/(BC)`
(2 ) Prove that ∆DEF is similar to ∆CBF Hence, find `(EF)/(FB)`.
(3) What is the ratio of the areas of ∆DEF and ∆BFC.
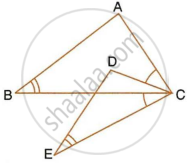
In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ∆ABC and ∆DEC.
The ratio between the altitudes of two similar triangles is 3 : 5; write the ratio between their :
- corresponding medians.
- perimeters.
- areas.
The ratio between the areas of two similar triangles is 16 : 25. State the ratio between their :
- perimeters.
- corresponding altitudes.
- corresponding medians.
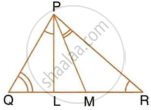
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that:
- ΔPQL ∼ ΔRPM
- QL × RM = PL × PM
- PQ2 = QR × QL
A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to ΔDEF such that the longest side of ΔDEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of ΔDEF.
In the give figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that ΔABC ∼ ΔEBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the:
- length of AB
- area of ΔABC

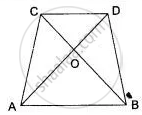
In fig. ABCD is a trapezium in which AB | | DC and AB = 2DC. Determine the ratio between the areas of ΔAOB and ΔCOD.