Advertisements
Advertisements
Question
In the given figure, AX : XB = 3 : 5
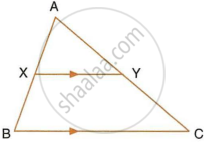
Find:
- the length of BC, if the length of XY is 18 cm.
- the ratio between the areas of trapezium XBCY and triangle ABC.
Solution
Given,
`(AX)/(XB) = 3/5 => (AX)/(AB) = 3/8` ...(1)
i. In ΔAXY and ΔABC,
As XY || BC, Corresponding angles are equal
∠AXY = ∠ABC
∠AYX = ∠ACB
ΔAXY ~ ΔABC
`=> (AX)/(AB) = (XY)/(BC)`
`=> 3/8 = 18/(BC)`
`=>` BC = 48 cm
ii. `"Area of ΔAXY"/"Area of ΔABC" = (AX^2)/(AB^2) = 9/64`
`"Area of ΔABC – Area of ΔAXY"/"Area of ΔABC" = (64 - 9)/64 = 55/64`
`"Area of trapezium XBCY"/"Area of ΔABC" = 55/64`
APPEARS IN
RELATED QUESTIONS
Given: ABCD is a rhombus, DPR and CBR are straight lines.
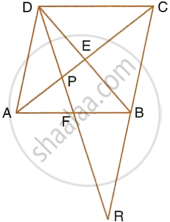
Prove that: DP × CR = DC × PR.
In ∆ABC, ∠B = 90° and BD ⊥ AC.
- If CD = 10 cm and BD = 8 cm; find AD.
- If AC = 18 cm and AD = 6 cm; find BD.
- If AC = 9 cm and AB = 7 cm; find AD.
Given : AB || DE and BC || EF. Prove that :
- `(AD)/(DG) = (CF)/(FG)`
- ∆DFG ∼ ∆ACG
In the given figure, P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC.
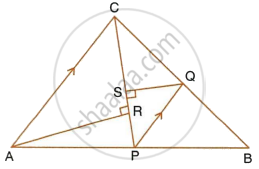
- Calculate the ratio PQ : AC, giving reason for your answer.
- In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°. Given QS = 6 cm, calculate the length of AR.
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB)=3/2`
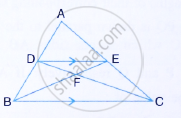
(1) Determine the ratios `(AD)/(AB) and (DE)/(BC)`
(2 ) Prove that ∆DEF is similar to ∆CBF Hence, find `(EF)/(FB)`.
(3) What is the ratio of the areas of ∆DEF and ∆BFC.
In the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.
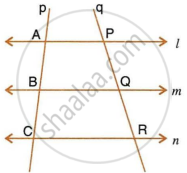
Prove that : `(AB)/(BC) = (PQ)/(QR)`
The dimensions of the model of a multistoreyed building are 1 m by 60 cm by 1.20 m. If the scale factor is 1 : 50, find the actual dimensions of the building.
Also, find:
- the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq. cm.
- the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m3.
A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to ΔDEF such that the longest side of ΔDEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of ΔDEF.
The following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively.
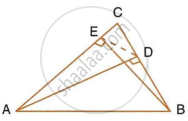
Show that:
- ΔADC ∼ ΔBEC
- CA × CE = CB × CD
- ΔABC ~ ΔDEC
- CD × AB = CA × DE
In the given figure, ABC is a right angled triangle with ∠BAC = 90°.
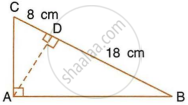
- Prove that : ΔADB ∼ ΔCDA.
- If BD = 18 cm and CD = 8 cm, find AD.
- Find the ratio of the area of ΔADB is to area of ΔCDA.
