Advertisements
Advertisements
Question
The following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively.
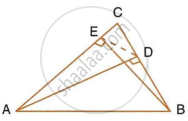
Show that:
- ΔADC ∼ ΔBEC
- CA × CE = CB × CD
- ΔABC ~ ΔDEC
- CD × AB = CA × DE
Solution
i. ∠ADC = ∠BEC = 90°
∠ACD = ∠BCE ...(Common)
ΔADC ∼ ΔBEC ...(AA similarity)
ii From part (i),
`(AC)/(BC) = (CD)/(EC)` ...(1)
`=>` CA × CE = CB × CD
iii. In ΔABC and ΔDEC,
From (1),
`(AC)/(BC) = (CD)/(EC) => (AC)/(CD) = (BC)/(EC)`
∠DCE = ∠BCA ...(Common)
ΔABC ~ ΔDEC ...(SAS similarity)
iv. From part (iii),
`(AC)/(DC) = (AB)/(DE)`
`=>` CD × AB = CA × DE
APPEARS IN
RELATED QUESTIONS
In ∆ABC, right – angled at C, CD ⊥ AB.
Prove:
`"CD"^2 = "AD"xx "DB"`
In ∆ABC, ∠B = 90° and BD ⊥ AC.
- If CD = 10 cm and BD = 8 cm; find AD.
- If AC = 18 cm and AD = 6 cm; find BD.
- If AC = 9 cm and AB = 7 cm; find AD.
In the given figure, P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC.
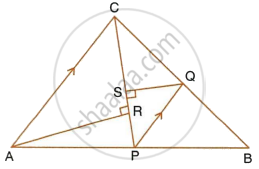
- Calculate the ratio PQ : AC, giving reason for your answer.
- In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°. Given QS = 6 cm, calculate the length of AR.
In the right-angled triangle QPR, PM is an altitude.
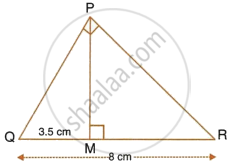
Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.
In the given figure, AX : XB = 3 : 5
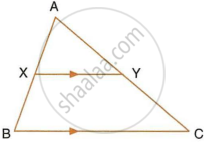
Find:
- the length of BC, if the length of XY is 18 cm.
- the ratio between the areas of trapezium XBCY and triangle ABC.
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produces at Q. Given the area of triangle CPQ = 20 cm2.

Calculate:
- area of triangle CDP,
- area of parallelogram ABCD.
An aeroplane is 30 m long and its model is 15 cm long. If the total outer surface area of the model is 150 cm2, find the cost of painting the outer surface of the aeroplane at the rate of Rs.120 per sq. m. Given that 50 sq. m of the surface of the aeroplane is left for windows.
The ratio between the areas of two similar triangles is 16 : 25. State the ratio between their :
- perimeters.
- corresponding altitudes.
- corresponding medians.
The dimensions of the model of a multistoreyed building are 1 m by 60 cm by 1.20 m. If the scale factor is 1 : 50, find the actual dimensions of the building.
Also, find:
- the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq. cm.
- the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m3.
A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to ΔDEF such that the longest side of ΔDEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of ΔDEF.
