Advertisements
Advertisements
Question
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produces at Q. Given the area of triangle CPQ = 20 cm2.

Calculate:
- area of triangle CDP,
- area of parallelogram ABCD.
Solution
i. In ΔBPQ and ΔCPD
∠BPQ = ∠CPD ...(Vertically opposite angles)
∠BQP = ∠PDC ...(Alternate angles)
ΔBPQ ~ ΔCPD ...(AA similarity)
∴ `(BP)/(PC) = (PQ)/(PD) = (BQ)/(CD) = 1/2` ...`(∵ (BP)/(PC) = 1/2)`
Also, `(ar(ΔBPQ))/(ar(ΔCPD)) = ((BP)/(PC))^2`
`=> 10/(ar(ΔCPD)) = 1/4` ...`[ar(ΔBPQ) = 1/2 xx ar(ΔCPQ), ar(CPQ) = 20]`
`=>` ar(∆CPD) = 40 cm2
ii. In ∆BAP and ∆AQD
As BP || AD, corresponding angles are equal
∠QBP = ∠QAD
∠BQP = ∠AQD ...(Common)
∆BQP ~ ∆AQD ...(AA similarity)
∴ `(AQ)/(BQ) = (QD)/(QP) = (AD)/(BP) = 3` ...`(∵ (BP)/(PC) = (PQ)/(PD) = 1/2 => (PQ)/(QD) = 1/3)`
Also, `(ar(ΔAQD))/(ar(ΔBQP))=((AQ)/(BQ))^2`
`=> (ar(ΔAQD))/10 = 9`
`=>` ar(∆AQD) = 90 cm2
∴ ar(ADPB) = ar(∆AQD) – ar(∆BQP)
= 90 cm2 – 10 cm2
= 80 cm2
ar(ABCD) = ar(∆CDP) + ar(ADPB)
= 40 cm2 + 80 cm2
= 120 cm2
APPEARS IN
RELATED QUESTIONS
Given: RS and PT are altitudes of ΔPQR. Prove that:
- ΔPQT ~ ΔQRS,
- PQ × QS = RQ × QT.
In ∆ ABC, ∠B = 2 ∠C and the bisector of angle B meets CA at point D. Prove that:
(i) ∆ ABC and ∆ ABD are similar,
(ii) DC: AD = BC: AB
In ∆ABC, right – angled at C, CD ⊥ AB.
Prove:
`"CD"^2 = "AD"xx "DB"`
In ∆ABC, ∠B = 90° and BD ⊥ AC.
- If CD = 10 cm and BD = 8 cm; find AD.
- If AC = 18 cm and AD = 6 cm; find BD.
- If AC = 9 cm and AB = 7 cm; find AD.
Given : AB || DE and BC || EF. Prove that :
- `(AD)/(DG) = (CF)/(FG)`
- ∆DFG ∼ ∆ACG
In the right-angled triangle QPR, PM is an altitude.
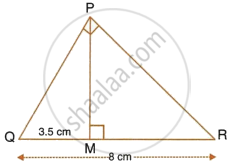
Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.
In the given figure, AX : XB = 3 : 5
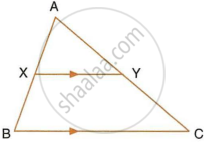
Find:
- the length of BC, if the length of XY is 18 cm.
- the ratio between the areas of trapezium XBCY and triangle ABC.
In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ∆ABC and ∆DEC.
The ratio between the altitudes of two similar triangles is 3 : 5; write the ratio between their :
- corresponding medians.
- perimeters.
- areas.
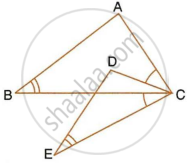
In the give figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that ΔABC ∼ ΔEBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the:
- length of AB
- area of ΔABC

