Advertisements
Advertisements
प्रश्न
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produces at Q. Given the area of triangle CPQ = 20 cm2.

Calculate:
- area of triangle CDP,
- area of parallelogram ABCD.
उत्तर
i. In ΔBPQ and ΔCPD
∠BPQ = ∠CPD ...(Vertically opposite angles)
∠BQP = ∠PDC ...(Alternate angles)
ΔBPQ ~ ΔCPD ...(AA similarity)
∴ `(BP)/(PC) = (PQ)/(PD) = (BQ)/(CD) = 1/2` ...`(∵ (BP)/(PC) = 1/2)`
Also, `(ar(ΔBPQ))/(ar(ΔCPD)) = ((BP)/(PC))^2`
`=> 10/(ar(ΔCPD)) = 1/4` ...`[ar(ΔBPQ) = 1/2 xx ar(ΔCPQ), ar(CPQ) = 20]`
`=>` ar(∆CPD) = 40 cm2
ii. In ∆BAP and ∆AQD
As BP || AD, corresponding angles are equal
∠QBP = ∠QAD
∠BQP = ∠AQD ...(Common)
∆BQP ~ ∆AQD ...(AA similarity)
∴ `(AQ)/(BQ) = (QD)/(QP) = (AD)/(BP) = 3` ...`(∵ (BP)/(PC) = (PQ)/(PD) = 1/2 => (PQ)/(QD) = 1/3)`
Also, `(ar(ΔAQD))/(ar(ΔBQP))=((AQ)/(BQ))^2`
`=> (ar(ΔAQD))/10 = 9`
`=>` ar(∆AQD) = 90 cm2
∴ ar(ADPB) = ar(∆AQD) – ar(∆BQP)
= 90 cm2 – 10 cm2
= 80 cm2
ar(ABCD) = ar(∆CDP) + ar(ADPB)
= 40 cm2 + 80 cm2
= 120 cm2
APPEARS IN
संबंधित प्रश्न
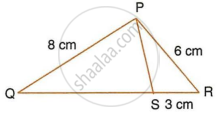
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
- Prove ΔPQR ∼ ΔSPR.
- Find the length of QR and PS.
- `"area of ΔPQR"/"area of ΔSPR"`
In ∆ABC, right – angled at C, CD ⊥ AB.
Prove:
`"CD"^2 = "AD"xx "DB"`
In the given triangle PQR, LM is parallel to QR and PM : MR = 3 : 4.
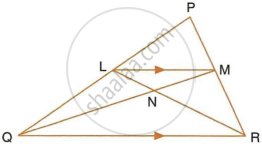
Calculate the value of ratio:
- `(PL)/(PQ)` and then `(LM)/(QR)`
- `"Area of ΔLMN"/"Area of ΔMNR"`
- `"Area of ΔLQM"/"Area of ΔLQN"`
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB)=3/2`
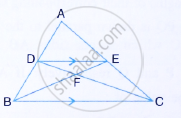
(1) Determine the ratios `(AD)/(AB) and (DE)/(BC)`
(2 ) Prove that ∆DEF is similar to ∆CBF Hence, find `(EF)/(FB)`.
(3) What is the ratio of the areas of ∆DEF and ∆BFC.
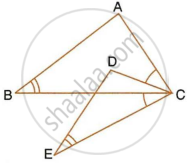
In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ∆ABC and ∆DEC.
In the following figure, AB, CD and EF are parallel lines. AB = 6cm, CD = y cm, EF = 10 cm, AC = 4 cm and CF = x cm. Calculate x and y 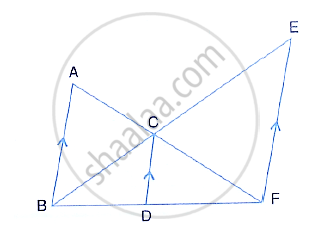
On a map, drawn to a scale of 1 : 20000, a rectangular plot of land ABCD has AB = 24 cm and BC = 32 cm. Calculate :
- the diagonal distance of the plot in kilometer.
- the area of the plot in sq. km.
The dimensions of the model of a multistoreyed building are 1 m by 60 cm by 1.20 m. If the scale factor is 1 : 50, find the actual dimensions of the building.
Also, find:
- the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq. cm.
- the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m3.
In the given figure, ABC is a right angled triangle with ∠BAC = 90°.
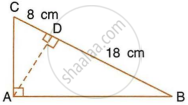
- Prove that : ΔADB ∼ ΔCDA.
- If BD = 18 cm and CD = 8 cm, find AD.
- Find the ratio of the area of ΔADB is to area of ΔCDA.
In fig. ABCD is a trapezium in which AB | | DC and AB = 2DC. Determine the ratio between the areas of ΔAOB and ΔCOD.