Advertisements
Advertisements
Question
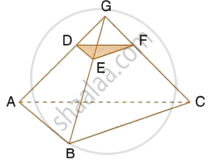
Given : AB || DE and BC || EF. Prove that :
- `(AD)/(DG) = (CF)/(FG)`
- ∆DFG ∼ ∆ACG
Solution
i. In ΔAGB, DE || AB, by Basic proportionality theorem
`(GD)/(DA) = (GE)/(EB)` ...(1)
In ΔGBC, EF || BC, by Basic proportionality theorem,
`(GE)/(EB) = (GF)/(FC)` ...(2)
From (1) and (2), we get
`(GD)/(DA) = (GF)/(FC)`
`(AD)/(DG) = (CF)/(FG)`
ii.
From (i), we have:
`(AD)/(DG) = (CF)/(FG)`
∠DGF = ∠AGC ...(Common)
∴ ΔDFG ∼ ΔACG ...(SAS similarity)
APPEARS IN
RELATED QUESTIONS
Given: RS and PT are altitudes of ΔPQR. Prove that:
- ΔPQT ~ ΔQRS,
- PQ × QS = RQ × QT.
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the right-angled triangle QPR, PM is an altitude.
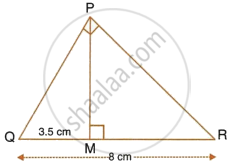
Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.
Triangle ABC is an isosceles triangle in which AB = AC = 13 cm and BC = 10 cm. AD is
perpendicular to BC. If CE = 8 cm and EF ⊥ AB, find:
i)`"area of ADC"/"area of FEB"` ii)`"area of ΔAFEB"/"area of ΔABC"`
In the given figure, triangle ABC is similar to triangle PQR. AM and PN are altitudes whereas AX and PY are medians.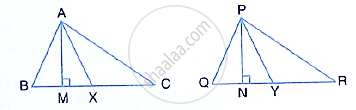
Prove that : `(AM)/(PN)=(AX)/(PY)`
In the following figure, AB, CD and EF are parallel lines. AB = 6cm, CD = y cm, EF = 10 cm, AC = 4 cm and CF = x cm. Calculate x and y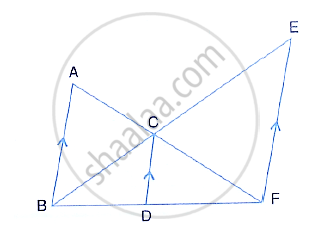 
On a map, drawn to a scale of 1 : 20000, a rectangular plot of land ABCD has AB = 24 cm and BC = 32 cm. Calculate :
- the diagonal distance of the plot in kilometer.
- the area of the plot in sq. km.
In ΔABC, ∠ACB = 90° and CD ⊥ AB.
Prove that : `(BC^2)/(AC^2)=(BD)/(AD)`
A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to ΔDEF such that the longest side of ΔDEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of ΔDEF.
In fig. ABCD is a trapezium in which AB | | DC and AB = 2DC. Determine the ratio between the areas of ΔAOB and ΔCOD.
