Advertisements
Advertisements
Question
The ratio between the areas of two similar triangles is 16 : 25. State the ratio between their :
- perimeters.
- corresponding altitudes.
- corresponding medians.
Solution
ΔABC ∼ ΔDEF, AL ⊥ BC and DM ⊥ EF and AP and DQ are the medians and also area ΔABC : area ΔDEF = 16 : 25
∵ ΔABC ~ ΔDEF ...(Given)
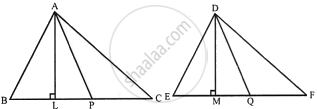
∴ `(Area ΔABC)/(Area ΔDEF) = (AB^2)/(DE^2)`
`\implies (AB^2)/(DE^2) = 16/25 = (4)^2/(5)^2`
∴ `(AB)/(DE) = 4/5` or AB : DE = 4 : 5 ...(i)
∵ ΔABC ∼ ΔDEF
∴ ∠B = ∠E and `(AB)/(DE) = (BC)/(EF)` ...(i)
i. ∵ ΔABC ∼ ΔDEF
∴ `(AB)/(DE) = (BC)/(EF) = (CA)/(FD)`
= `(AB + BC + CA)/(DE + EF + FD)`
= `4/5` ...[From (i)]
∴ The ratio between two perimeters = 4 : 5
ii. Now, in ΔABC and ΔDEM,
∴ ∠B = ∠E, ∠L = ∠M ...(Each 90°)
∴ ΔABL ∼ ΔDEM ...(AA criterion of similarity)
∴ `(AB)/(DE) = (AL)/(DM) = 4/5` ...[From (i)]
∵ AL : DM = 4 : 5
iii. ΔABC ∼ ΔDEF, ∠B = ∠E and
`(AB)/(DE) = (BC)/(EF) = (2BP)/(2EQ) = (BP)/(EQ)`
∴ ΔABD ∼ ΔDEQ
∴ `(AB)/(DE) = (AP)/(DQ) = 4/5` ...[From (i)]
∴ AB : DE = 4 : 5
APPEARS IN
RELATED QUESTIONS
Given: RS and PT are altitudes of ΔPQR. Prove that:
- ΔPQT ~ ΔQRS,
- PQ × QS = RQ × QT.
In ∆ ABC, ∠B = 2 ∠C and the bisector of angle B meets CA at point D. Prove that:
(i) ∆ ABC and ∆ ABD are similar,
(ii) DC: AD = BC: AB
In ∆ABC, ∠B = 90° and BD ⊥ AC.
- If CD = 10 cm and BD = 8 cm; find AD.
- If AC = 18 cm and AD = 6 cm; find BD.
- If AC = 9 cm and AB = 7 cm; find AD.
Given : AB || DE and BC || EF. Prove that :
- `(AD)/(DG) = (CF)/(FG)`
- ∆DFG ∼ ∆ACG
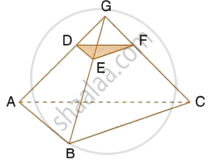
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the right-angled triangle QPR, PM is an altitude.
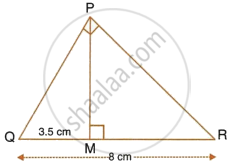
Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.
Triangle ABC is an isosceles triangle in which AB = AC = 13 cm and BC = 10 cm. AD is
perpendicular to BC. If CE = 8 cm and EF ⊥ AB, find:
i)`"area of ADC"/"area of FEB"` ii)`"area of ΔAFEB"/"area of ΔABC"`

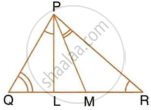
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that:
- ΔPQL ∼ ΔRPM
- QL × RM = PL × PM
- PQ2 = QR × QL
A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to ΔDEF such that the longest side of ΔDEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of ΔDEF.
In the given figure, ABC is a right angled triangle with ∠BAC = 90°.
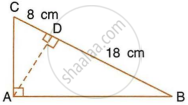
- Prove that : ΔADB ∼ ΔCDA.
- If BD = 18 cm and CD = 8 cm, find AD.
- Find the ratio of the area of ΔADB is to area of ΔCDA.
