Advertisements
Advertisements
प्रश्न
The ratio between the areas of two similar triangles is 16 : 25. State the ratio between their :
- perimeters.
- corresponding altitudes.
- corresponding medians.
उत्तर
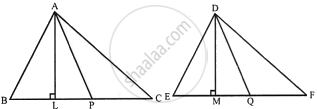
ΔABC ∼ ΔDEF, AL ⊥ BC and DM ⊥ EF and AP and DQ are the medians and also area ΔABC : area ΔDEF = 16 : 25
∵ ΔABC ~ ΔDEF ...(Given)
∴ `(Area ΔABC)/(Area ΔDEF) = (AB^2)/(DE^2)`
`\implies (AB^2)/(DE^2) = 16/25 = (4)^2/(5)^2`
∴ `(AB)/(DE) = 4/5` or AB : DE = 4 : 5 ...(i)
∵ ΔABC ∼ ΔDEF
∴ ∠B = ∠E and `(AB)/(DE) = (BC)/(EF)` ...(i)
i. ∵ ΔABC ∼ ΔDEF
∴ `(AB)/(DE) = (BC)/(EF) = (CA)/(FD)`
= `(AB + BC + CA)/(DE + EF + FD)`
= `4/5` ...[From (i)]
∴ The ratio between two perimeters = 4 : 5
ii. Now, in ΔABC and ΔDEM,
∴ ∠B = ∠E, ∠L = ∠M ...(Each 90°)
∴ ΔABL ∼ ΔDEM ...(AA criterion of similarity)
∴ `(AB)/(DE) = (AL)/(DM) = 4/5` ...[From (i)]
∵ AL : DM = 4 : 5
iii. ΔABC ∼ ΔDEF, ∠B = ∠E and
`(AB)/(DE) = (BC)/(EF) = (2BP)/(2EQ) = (BP)/(EQ)`
∴ ΔABD ∼ ΔDEQ
∴ `(AB)/(DE) = (AP)/(DQ) = 4/5` ...[From (i)]
∴ AB : DE = 4 : 5
APPEARS IN
संबंधित प्रश्न
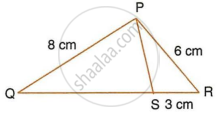
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
- Prove ΔPQR ∼ ΔSPR.
- Find the length of QR and PS.
- `"area of ΔPQR"/"area of ΔSPR"`
In ∆ ABC, ∠B = 2 ∠C and the bisector of angle B meets CA at point D. Prove that:
(i) ∆ ABC and ∆ ABD are similar,
(ii) DC: AD = BC: AB
In ∆PQR, ∠Q = 90° and QM is perpendicular to PR. Prove that:
- PQ2 = PM × PR
- QR2 = PR × MR
- PQ2 + QR2 = PR2
In ∆ABC, ∠B = 90° and BD ⊥ AC.
- If CD = 10 cm and BD = 8 cm; find AD.
- If AC = 18 cm and AD = 6 cm; find BD.
- If AC = 9 cm and AB = 7 cm; find AD.
Given : AB || DE and BC || EF. Prove that :
- `(AD)/(DG) = (CF)/(FG)`
- ∆DFG ∼ ∆ACG
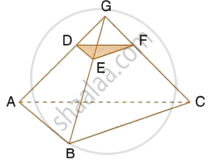
In the given figure, P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC.
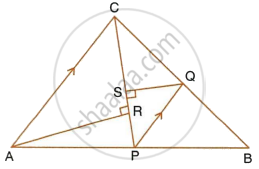
- Calculate the ratio PQ : AC, giving reason for your answer.
- In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°. Given QS = 6 cm, calculate the length of AR.
On a map, drawn to a scale of 1 : 20000, a rectangular plot of land ABCD has AB = 24 cm and BC = 32 cm. Calculate :
- the diagonal distance of the plot in kilometer.
- the area of the plot in sq. km.
Two isosceles triangles have equal vertical angles. Show that the triangles are similar. If the ratio between the areas of these two triangles is 16 : 25, find the ratio between their corresponding altitudes.
In the give figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that ΔABC ∼ ΔEBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the:
- length of AB
- area of ΔABC

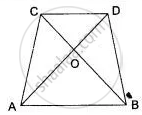
In fig. ABCD is a trapezium in which AB | | DC and AB = 2DC. Determine the ratio between the areas of ΔAOB and ΔCOD.