Advertisements
Advertisements
प्रश्न
In ∆PQR, ∠Q = 90° and QM is perpendicular to PR. Prove that:
- PQ2 = PM × PR
- QR2 = PR × MR
- PQ2 + QR2 = PR2
उत्तर

i. In ∆PQM and ∆PQR,
∠PMQ = ∠PQR = 90°
∠QPM = ∠RPQ ...(Common)
∴ ∆PQM ~ ∆PRQ ...(By AA Similarity)
∴ `(PQ)/(PR) = (PM)/(PQ)`
`=>` PQ2 = PM × PR
ii. In ∆QMR and ∆PQR,
∠QMR = ∠PQR = 90°
∠QRM = ∠QRP ...(Common)
∴ ∆QRM ~ ∆PQR ...(By AA similarity)
∴ `(QR)/(PR) = (MR)/(QR)`
`=>` QR2 = PR × MR
iii. Adding the relations obtained in (i) and (ii), we get,
PQ2 + QR2 = PM × PR + PR × MR
= PR(PM + MR)
= PR × PR
= PR2
APPEARS IN
संबंधित प्रश्न
Given: RS and PT are altitudes of ΔPQR. Prove that:
- ΔPQT ~ ΔQRS,
- PQ × QS = RQ × QT.
In ∆ABC, right – angled at C, CD ⊥ AB.
Prove:
`"CD"^2 = "AD"xx "DB"`
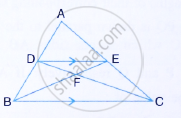
Given : AB || DE and BC || EF. Prove that :
- `(AD)/(DG) = (CF)/(FG)`
- ∆DFG ∼ ∆ACG
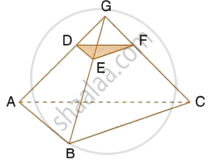
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB)=3/2`
(1) Determine the ratios `(AD)/(AB) and (DE)/(BC)`
(2 ) Prove that ∆DEF is similar to ∆CBF Hence, find `(EF)/(FB)`.
(3) What is the ratio of the areas of ∆DEF and ∆BFC.
Triangle ABC is an isosceles triangle in which AB = AC = 13 cm and BC = 10 cm. AD is
perpendicular to BC. If CE = 8 cm and EF ⊥ AB, find:
i)`"area of ADC"/"area of FEB"` ii)`"area of ΔAFEB"/"area of ΔABC"`

In the following figure, AB, CD and EF are parallel lines. AB = 6cm, CD = y cm, EF = 10 cm, AC = 4 cm and CF = x cm. Calculate x and y 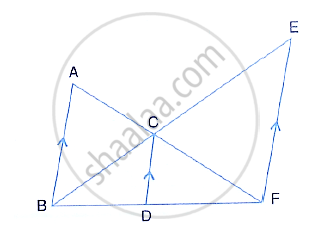
The dimensions of the model of a multistoreyed building are 1 m by 60 cm by 1.20 m. If the scale factor is 1 : 50, find the actual dimensions of the building.
Also, find:
- the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq. cm.
- the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m3.
In ΔABC, ∠ACB = 90° and CD ⊥ AB.
Prove that : `(BC^2)/(AC^2)=(BD)/(AD)`
A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to ΔDEF such that the longest side of ΔDEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of ΔDEF.
In fig. ABCD is a trapezium in which AB | | DC and AB = 2DC. Determine the ratio between the areas of ΔAOB and ΔCOD.