Advertisements
Advertisements
प्रश्न
In ∆ABC, ∠B = 90° and BD ⊥ AC.
- If CD = 10 cm and BD = 8 cm; find AD.
- If AC = 18 cm and AD = 6 cm; find BD.
- If AC = 9 cm and AB = 7 cm; find AD.
उत्तर
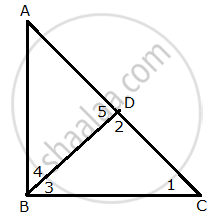
i. In ∆CDB,
∠1 + ∠2 + ∠3 = 180°
∠1 + ∠3 = 90° ...(1) (Since, ∠2 = 90°)
∠3 + ∠4 = 90° ...(2) (Since, ∠ABC = 90°)
From (1) and (2),
∠1 + ∠3 = ∠3 + ∠4
∠1 = ∠4
Also, ∠2 = ∠5 = 90°
∴ ∆CDB ~ ∆BDA ...(By AA similarity)
`=> (CD)/(BD) = (BD)/(AD)`
`=>` BD2 = AD × CD
`=>` (8)2 = AD × 10
`=>` AD = 6.4
Hence, AD = 6.4 cm
ii. Also, by similarity, we have:
`(BD)/(DA) = (CD)/(BD)`
BD2 = 6 × (18 – 6)
BD2 = 72
Hence, BD = 8.5 cm
iii. Clearly, ∆ADB ~ ∆ABC
`∴(AD)/(AB)=(AB)/(AC)`
`AD = (7 xx 7)/9`
= `(49)/9`
= `5 4/9`
Hence, `AD = 5 4/9 cm`
APPEARS IN
संबंधित प्रश्न
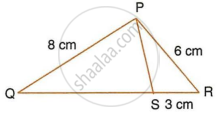
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
- Prove ΔPQR ∼ ΔSPR.
- Find the length of QR and PS.
- `"area of ΔPQR"/"area of ΔSPR"`
In ∆PQR, ∠Q = 90° and QM is perpendicular to PR. Prove that:
- PQ2 = PM × PR
- QR2 = PR × MR
- PQ2 + QR2 = PR2
In the given figure, P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC.
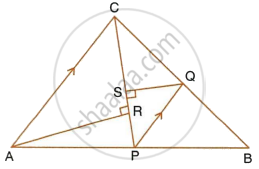
- Calculate the ratio PQ : AC, giving reason for your answer.
- In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°. Given QS = 6 cm, calculate the length of AR.
In the given figure, AX : XB = 3 : 5
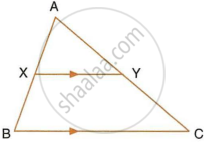
Find:
- the length of BC, if the length of XY is 18 cm.
- the ratio between the areas of trapezium XBCY and triangle ABC.
Triangle ABC is an isosceles triangle in which AB = AC = 13 cm and BC = 10 cm. AD is
perpendicular to BC. If CE = 8 cm and EF ⊥ AB, find:
i)`"area of ADC"/"area of FEB"` ii)`"area of ΔAFEB"/"area of ΔABC"`

In the following figure, AB, CD and EF are parallel lines. AB = 6cm, CD = y cm, EF = 10 cm, AC = 4 cm and CF = x cm. Calculate x and y 
The dimensions of the model of a multistoreyed building are 1 m by 60 cm by 1.20 m. If the scale factor is 1 : 50, find the actual dimensions of the building.
Also, find:
- the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq. cm.
- the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m3.
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that:
- ΔPQL ∼ ΔRPM
- QL × RM = PL × PM
- PQ2 = QR × QL
Two isosceles triangles have equal vertical angles. Show that the triangles are similar. If the ratio between the areas of these two triangles is 16 : 25, find the ratio between their corresponding altitudes.
In triangle ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA.
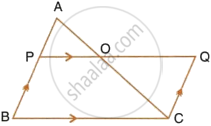
Find:
- area ΔAPO : area ΔABC.
- area ΔAPO : area ΔCQO.
