Advertisements
Advertisements
प्रश्न
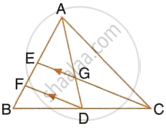
In the following figure, AD and CE are medians of ΔABC. DF is drawn parallel to CE. Prove that :
- EF = FB,
- AG : GD = 2 : 1
उत्तर
i. In ∆BFD and ∆BEC,
∠BFD = ∠BEC ...(Corresponding angles)
∠FBD = ∠EBC ...(Common)
∆BFD ~ ∆BEC ...(AA Similarity)
∴ `(BF)/(BE) = (BD)/(BC)`
`(BF)/(BE) = 1/2` ...(As D is the mid-point of BC)
BE = 2BF
BF = FE = 2BF
Hence, EF = FB
ii. In ΔAFD, EG || FD.
Using Basic Proportionality theorem,
`(AE)/(EF) = (AG)/(GD)` ...(1)
Now, AE = EB ...(As E is the mid-point of AB)
AE = 2EF ...(Since, EF = FB, by (i))
From (1),
`(AG)/(GD) = 2/1`
Hence, AG : GD = 2 : 1
APPEARS IN
संबंधित प्रश्न
In ∆ ABC, ∠B = 2 ∠C and the bisector of angle B meets CA at point D. Prove that:
(i) ∆ ABC and ∆ ABD are similar,
(ii) DC: AD = BC: AB
In ∆ABC, ∠B = 90° and BD ⊥ AC.
- If CD = 10 cm and BD = 8 cm; find AD.
- If AC = 18 cm and AD = 6 cm; find BD.
- If AC = 9 cm and AB = 7 cm; find AD.
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB)=3/2`
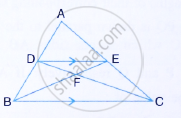
(1) Determine the ratios `(AD)/(AB) and (DE)/(BC)`
(2 ) Prove that ∆DEF is similar to ∆CBF Hence, find `(EF)/(FB)`.
(3) What is the ratio of the areas of ∆DEF and ∆BFC.
The ratio between the altitudes of two similar triangles is 3 : 5; write the ratio between their :
- corresponding medians.
- perimeters.
- areas.
The ratio between the areas of two similar triangles is 16 : 25. State the ratio between their :
- perimeters.
- corresponding altitudes.
- corresponding medians.
On a map, drawn to a scale of 1 : 20000, a rectangular plot of land ABCD has AB = 24 cm and BC = 32 cm. Calculate :
- the diagonal distance of the plot in kilometer.
- the area of the plot in sq. km.
In ΔABC, ∠ACB = 90° and CD ⊥ AB.
Prove that : `(BC^2)/(AC^2)=(BD)/(AD)`
A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to ΔDEF such that the longest side of ΔDEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of ΔDEF.
In triangle ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA.
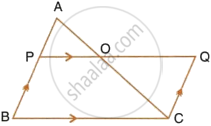
Find:
- area ΔAPO : area ΔABC.
- area ΔAPO : area ΔCQO.
In the given figure, ABC is a right angled triangle with ∠BAC = 90°.
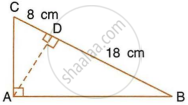
- Prove that : ΔADB ∼ ΔCDA.
- If BD = 18 cm and CD = 8 cm, find AD.
- Find the ratio of the area of ΔADB is to area of ΔCDA.
