Question

The two similar triangles are equal in area. Prove that the triangles are congruent.

Answer 1

Given: ΔABC ∼ ΔPQR and are equal in area

To prove: ΔABC ≅ ΔPQR

Proof: ∵ ΔABC ∼ ΔPQR

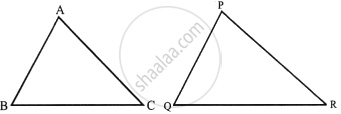
∴ `(Area  ΔABC)/(Area  ΔPQR) = (AB^2)/(PQ^2) = (BC^2)/(QR^2) = (AC^2)/(PR^2)`

But Area ΔABC = Area ΔPQR   ...(Given)

∴ `(AB^2)/(PQ^2) = (BC^2)/(QR^2) = (AC^2)/(PR^2) = 1`

`\implies (AB^2)/(PQ^2) = 1,`

`\implies` AB² = PQ²

`\implies` AB = PQ

Similarly, BC = QR and AC = PR

Now in ΔABC and ΔPQR

AB = PQ, BC = QR, AC = PR  ...(Proved)

∴ ΔABC ≅ ΔPQR  ...(SSS criterion of congruency)