Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 8cm, AB = 12cm and AE = 12cm, find CE.
उत्तर
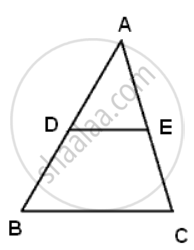
In ΔADE and ΔABC
∠D = ∠B and ∠C = ∠E ...(DE || BC)
⇒ ΔADE ∼ ΔABC
∴ `"AD"/"DB" = "AE"/"EC"`
DB
= AB - AD
= 12 - 8
= 4
⇒ `(8)/(4) = (12)/"EC"`
⇒ 8 x EC = 12 x 4
⇒ EC = `(12 xx 4)/(8)`
⇒ EC = 6cm.
APPEARS IN
संबंधित प्रश्न
The diagonals of a quadrilateral ABCD intersect each other at the point O such that `("AO")/("BO") = ("CO")/("DO")`. Show that ABCD is a trapezium.
In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
- Prove that ΔACD is similar to ΔBCA.
- Find BC and CD.
- Find area of ΔACD : area of ΔABC.
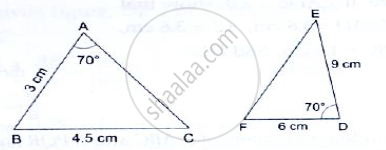
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
State the SSS-similarity criterion for similarity of triangles
∆ABC and ∆DEF are equilateral triangles, A(∆ABC): A(∆DEF) = 1: 2. If AB = 4 then what is length of DE?

In the figure , ABCD is a quadrilateral . F is a point on AD such that AF = 2.1 cm and FD = 4.9 cm . E and G are points on AC and AB respectively such that EF || CD and GE || BC . Find `("Ar" triangle "BCD")/("Ar" triangle "GEF")`
A line segment DE is drawn parallel to base BC of ΔABC which cuts AB at point D and AC at point E. If AB = 5BD and EC = 3.2 cm, find the length of AE.
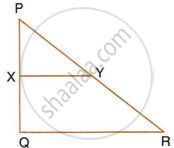
In the figure, given below, PQR is a right-angle triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.
If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AB = 5.6cm, AD = 1.4cm, AC = 7.2cm, and AE = 1.8cm
In the figure, AB || RQ and BC || SQ, prove that `"PC"/"PS" = "PA"/"PR"`.