Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3,Find x.
उत्तर
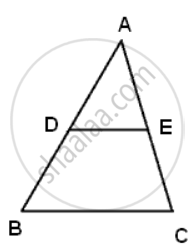
In ΔADE and ΔABC
∠D = ∠B and ∠C = ∠E ...(DE || BC)
⇒ ΔADE ∼ ΔABC
∴ `"AD"/"DB" = "AE"/"EC"`
⇒ `(4x - 3)/(3x - 1) = (8x - 7)/(5x - 3)`
⇒ (4x - 3) x (5x - 3) = (8x - 7) x (3x - 1)
⇒ 20x2 - 15x - 12x + 9 = 24x2 - 21x - 8x + 7
⇒ 20x2 - 27x + 9 = 24x2 29x + 7
⇒ 4x2 - 2x - 2 = 0
⇒ `x(x - 1) + (1)/(2)(x - 1)` = 0
⇒ `(x + 1/2)` = 0; x - 1 = 0
⇒ x = `-(1)/(2); x = 1`
∴ x = 1.
APPEARS IN
संबंधित प्रश्न
State, true or false:
All equiangular triangles are similar.
Prove that the area of Δ BCE described on one side BC of a square ABCD is one half the area of the similar Δ ACF described on the diagonal AC.
In MBC, DE is drawn parallel to BC. If AD: DB=2:3, DE =6cm and AE =3.6cm, find BC and AC.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OC', if OC = 21 cm.
Also, state the value of :
- `(OB^')/(OB)`
- `(C^'A^')/(CA)`
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AE)/(AC)`

Let ∆ ABC ∽ ∆ DEF and their areas be respectively, 64 cm2 and 121 cm2. If EF = 15⋅4 cm, find BC.
Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AD"/"AB"`
Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
In triangle ABC point D is on side BC (B−D−C) such that ∠BAC = ∠ADC then prove that CA2 = CB × CD