Advertisements
Advertisements
प्रश्न
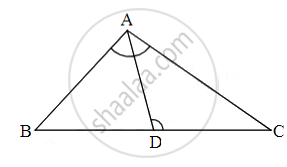
In triangle ABC point D is on side BC (B−D−C) such that ∠BAC = ∠ADC then prove that CA2 = CB × CD
उत्तर
In ΔBAC and ΔADC,
∠BAC ≅ ∠ADC ......[Given]
∠BCA ≅ ∠ACD ......[Common angle]
∴ ΔBAC ∼ ΔADC .....[AA test of similarity]
∴ `"CA"/"CD" = "CB"/"CA"` ......[Corresponding sides of similar triangles]
∴ CA × CA = CB × CD
∴ CA2 = CB × CD
APPEARS IN
संबंधित प्रश्न
In figure, if ∠A = ∠C, then prove that ∆AOB ~ ∆COD

A vertical pole of length 7.5 cm casts a shadow 5 m long on the ground and at the same time a tower casts a shadow 24 m long. Find the height of the tower.
State the AA-similarity criterion
In the given figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF.

Proof : In ΔXDE, PQ || DE ...`square`
∴ `"XP"/square = square/"QE"` ...(I) (Basic proportionality theorem)
In ΔXEF, QR || EF ...`square`
∴ `square/square = square/square ..."(II)" square`
∴ `square/square = square/square` ...from (I) and (II)
∴ seg PR || seg DF ...(converse of basic proportionality theorem)
ΔABC ∼ ΔDEF and A(ΔABC) : A Δ(DEF) = 1 : 2 If AB = 4 find DE.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 8cm, AB = 12cm and AE = 12cm, find CE.
If ΔPQR, AB is drawn parallel to QR. If PQ = 9cm, PR = 6cm and PB = 4.cm, find the length of AP.
In the figure, AB || RQ and BC || SQ, prove that `"PC"/"PS" = "PA"/"PR"`.
D and E are points on the sides AB and AC of ΔABC such that DE | | BC and divides ΔABC into two parts, equal in area. Find `"BD"/"AB"`.
A plot of land of area 20km2 is represented on the map with a scale factor of 1:200000. Find: The area on the map that represented the plot of land.
A map is drawn to scale of 1:20000. Find: The distance on the map representing 4km
In ∆LMN, ∠L = 60°, ∠M = 50°. If ∆LMN ~ ∆PQR then the value of ∠R is
If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is
In the given figure YH || TE. Prove that ΔWHY ~ ΔWET and also find HE and TE
A flag pole 15 m high casts a shadow of 3 m at 10 a.m. The shadow cast by a building at the same time is 18.6 m. The height of the building is
In fig., seg AC and seg BD intersect each other at point P.

`"AP"/"PC" = "BP"/"PD"` then prove that ΔABP ~ ΔCDP
ΔABP ~ ΔDEF and A(ΔABP) : A(ΔDEF) = 144:81, then AB : DE = ?
Two triangles are similar. Smaller triangle’s sides are 4 cm, 5 cm, 6 cm. Perimeter of larger triangle is 90 cm then find the sides of larger triangle.
ΔDEF ~ ΔABC. If DE : AB = 2 : 3 and ar ΔDEF is equal to 44 square units then ar (ΔABC) (square unit) is ______.
In a square of side 10 cm, its diagonal = ______.
