Advertisements
Advertisements
प्रश्न
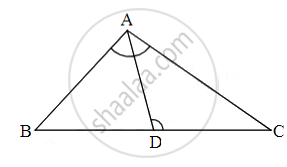
In triangle ABC point D is on side BC (B−D−C) such that ∠BAC = ∠ADC then prove that CA2 = CB × CD
उत्तर
In ΔBAC and ΔADC,
∠BAC ≅ ∠ADC ......[Given]
∠BCA ≅ ∠ACD ......[Common angle]
∴ ΔBAC ∼ ΔADC .....[AA test of similarity]
∴ `"CA"/"CD" = "CB"/"CA"` ......[Corresponding sides of similar triangles]
∴ CA × CA = CB × CD
∴ CA2 = CB × CD
APPEARS IN
संबंधित प्रश्न
State, true or false:
Two isosceles-right triangles are similar.
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB) = 3/2`.
- Determine the ratios `(AD)/(AB)` and `(DE)/(BC)`.
- Prove that ∆DEF is similar to ∆CBF. Hence, find `(EF)/(FB).`
- What is the ratio of the areas of ∆DEF and ∆BFC?
The corresponding sides of two similar triangles ABC and DEF are BC = 9.1cm and EF = 6.5cm. If the perimeter of ΔDEF is 25cm, find the perimeter of ΔABC.
In an isosceles ΔABC, the base AB is produced both ways in P and Q such that
AP × BQ = AC2.
Prove that ΔACP~ΔBCQ.

State the SAS-similarity criterion
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in cm, of the model; if the length of the aeroplane is 40 m.
In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find : PQ

If ΔABC ~ ΔDEF, then writes the corresponding congruent angles and also write the ratio of corresponding sides.
Construct a triangle ABC with side BC = 6 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are `(3)/(4)` times the corresponding sides of the ΔABC.
Points A(3, 1), B(5, 1), C(a, b) and D(4, 3) are vertices of a parallelogram ABCD. Find the values of a and b.
In the adjoining figure, the medians BD and CE of a ∆ABC meet at G. Prove that
(i) ∆EGD ∼ ∆CGB and
(ii) BG = 2GD for (i) above.
Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
In ΔABC, DE is drawn parallel to BC cutting AB in the ratio 2 : 3. Calculate:
(i) `("area"(Δ"ADE"))/("area"(Δ"ABC")`
(i) `("area"("trapeziumEDBC"))/("area"(Δ"ABC"))`
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The area of land represented on the map.
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆QMO

State whether the following triangles are similar or not: If yes, then write the test of similarity.
∠P = 35°, ∠X = 35° and ∠Q = 60°, ∠Y = 60°

ΔABC ~ ΔPQR, A(ΔABC) = 80 sq.cm, A(ΔPQR) = 125 sq.cm, then complete `("A"(Δ"ABC"))/("A"(Δ"PQR")) = 80/125 = (["______"])/(["______"])`, hence `"AB"/"PQ" = (["______"])/(["______"])`
In given fig., quadrilateral PQRS, side PQ || side SR, AR = 5 AP, then prove that, SR = 5PQ
In figure, if AD = 6cm, DB = 9cm, AE = 8cm and EC = 12cm and ∠ADE = 48°. Find ∠ABC.

