Advertisements
Advertisements
प्रश्न
Construct a triangle ABC with side BC = 6 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are `(3)/(4)` times the corresponding sides of the ΔABC.
उत्तर
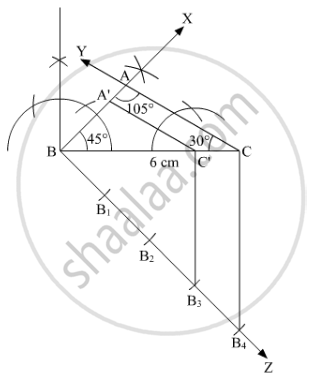
Steps of construction
(1) Draw BC = 6 cm.
(2) At point B, draw ∠XBC = 45°
(3) Using Angle Sum Property in ∆ABC,
∠A + ∠B + ∠C = 180°
105° + 45° + ∠C = 180°
∠C = 30°
And, now draw ∠YCB = 30°
(4) Now, line YC and XB intersect at point A. Thus this is our required triangle ABC.
(5) Draw an acute angle ∠CBZ at B.
(6) Now cut 4 equal arcs BB1, B1B2, B2B3, and B3B4 on BZ.
(7) Now, join B4 to C.
(8) Draw a line parallel to B4C from B3 which intersects BC at C'.
(9) Now, draw a line parallel to AC from C' which intersects BX at A'.
(10) Thus, ∆ABC is our required triangle whose sides are `(3)/(4)` times the corresponding sides of ΔABC.
APPEARS IN
संबंधित प्रश्न
In a triangle ABC, line l || Side BC and line l intersects side AB and AC in points P and Q, respectively. Prove that: `"AP"/"BP"="AQ"/"QC"`

P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm, PB = 6cm. AQ = 5 cm and QC = 10 cm, show that BC = 3PQ.
A vertical stick 20 cm long casts a shadow 6 cm long on the ground. At the same time, a tower casts a shadow 15 m long on the ground. Find the height of the tower.
In the following figure, DE || OQ and DF || OR, show that EF || QR.

The diagonals of a quadrilateral ABCD intersect each other at the point O such that `("AO")/("BO") = ("CO")/("DO")`. Show that ABCD is a trapezium.
`triangleDEF ~ triangleMNK`. If DE = 5 and MN = 6, then find the value of `(A(triangleDEF))/(A(triangleMNK))`
In the given figure ΔABC and ΔAMP are right angled at B and M respectively. Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
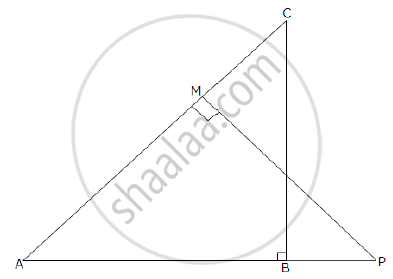
1) Prove ΔABC ~ ΔAMP
2) Find AB and BC.
In ΔABC and ΔDEF, it is being given that: AB = 5 cm, BC = 4 cm and CA = 4.2 cm; DE=10cm, EF = 8 cm and FD = 8.4 cm. If AL ⊥ BC and DM ⊥ EF, find AL: DM.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5,

Find:
- ∆APB : ∆CPB
- ∆DPC : ∆APB
- ∆ADP : ∆APB
- ∆APB : ∆ADB
Two chords AB and CD of a circle intersect at a point P outside the circle.
Prove that: (i) Δ PAC ~ Δ PDB (ii) PA. PB = PC.PD

State the SSS-similarity criterion for similarity of triangles
In Δ PQR, MN is drawn parallel to QR. If PM = x, MQ = (x-2), PN = (x+2) and NR = (x-1), find the value of x.
The length of a river in a map is 54cm. if lcm on the map represents 12500m on land, find the length of the river.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The area in km2 that can be represented by 1 cm2
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : A' B', if AB = 4 cm.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in cm, of the model; if the length of the aeroplane is 40 m.
On a map drawn to scale of 1 : 2,50,000 a rectangular plot of land ABCD has the following measurement AB = 12 cm, BC = 16 cm angles A, B, C, and D are 900 each. Calculate:
(i) The diagonal distance of the plot of land in
(ii) Actual length of diagonal.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4, AE = 8, DB = x - 4 and EC = 3x - 19, find x.
ΔABC is right angled at A. AD is drawn perpendicular to BC. If AB = 8cm and AC = 6cm, calculate BD.
A plot of land of area 20km2 is represented on the map with a scale factor of 1:200000. Find: The number of KM represented by 2cm on the map.
A map is drawn to scale of 1:20000. Find: The area of the lake on the map which has an actual area of 12km2
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The area of the plot in sq km
Check whether the triangles are similar and find the value of x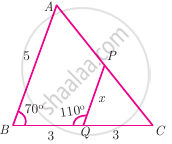
Construct a triangle similar to a given triangle PQR with its sides equal to `2/3` of the corresponding sides of the triangle PQR (scale factor `2/3 < 1`)
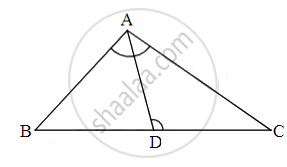
In triangle ABC point D is on side BC (B−D−C) such that ∠BAC = ∠ADC then prove that CA2 = CB × CD
An architecture have model of building. Length of building is 1 m then length of model is 0.75 cm. Then find length and height of model building whose actual length is 22.5 m and height is 10 m
In figure, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.
In ΔPQR, S and T are points on PQ and PR respectively. `(PS)/(SQ) = (PT)/(TR)` and ∠PST = ∠PRQ. Prove that PQR is an isosceles triangle.
