Advertisements
Advertisements
प्रश्न
ΔABC is right angled at A. AD is drawn perpendicular to BC. If AB = 8cm and AC = 6cm, calculate BD.
उत्तर
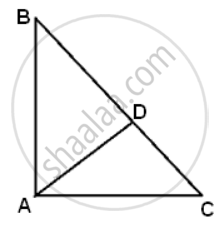
In ΔABC,
Using Pythagoras theorem
BC2 = AB2 + AC2
BC2 = 82 + 62
BC2 = 64 + 36
BC = `sqrt(100)` = 10..........(i)
In ΔABD,
Using Pythagoras theorem
AD2 = AB2 - BD2
AD2 = 82 - BD2......(ii)
In ΔACD,
Using Pythagoras theorem
AD2 = AC2 - CD2
AD2 = 62 - CD2......(iii)
Equaliting (ii) and (iii)
82 - BD2 = 62 - CD
∵ CD = BC - BD
82 - BD2 = 62 - (BC - BD)2
CD = BC - BD
BC = 10cm(from (i))
82 - BD2 = 62 - (10 - BD)2
82 - BD2 = 62 - (100 - 20BD + BD2)
64 + BD2 = 62 - (100 + 20BD - BD2)
64 = -64 + 20BD
20BD = 128
BD = 6.4cm.
APPEARS IN
संबंधित प्रश्न
In figure, `\frac{AO}{OC}=\frac{BO}{OD}=\frac{1}{2}` and AB = 5 cm. Find the value of DC.
Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
A model of a ship if made to a scale of 1 : 200.
(i) Thelength of the model is 4 m; calculate the length of the ship.
(ii) The area of the deck of the ship is 160000 m2; find the area of the deck of the model.
(iii) The volume of the model is 200 litres; calculate the volume of the ship in m3.
ΔABC~ΔPQR and ar(ΔABC) = 4, ar(ΔPQR) . If BC = 12cm, find QR.
In ΔABC, BP and CQ are altitudes from B and C on AC and AB respectively. BP and CQ intersect at O. Prove that
(i) PC x OQ = QB x OP
(ii) `"OC"^2/"OB"^2 = ("PC" xx "PO")/("QB" xx "QO")`
In a quadrilateral PQRS, the diagonals PR and QS intersect each other at the point T. If PT:TR = QT :TS = 1:2, show that ΔPTQ - DRTS
Check whether the triangles are similar and find the value of x
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 + c2 = `2"p"^2 + "a"^2/2`
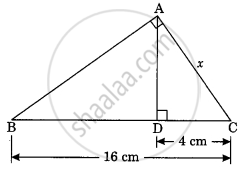
In the given figure the value of x is
If ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm and BC = 15 cm, then PR is equal to ______.
