Advertisements
Advertisements
प्रश्न
The sides PQ and PR of the ΔPQR are produced to S and T respectively. ST is drawn parallel to QR and PQ: PS = 3:4. If PT = 9.6 cm, find PR. If 'p' be the length of the perpendicular from P to QR, find the length of the perpendicular from P to ST in terms of 'p'.
उत्तर
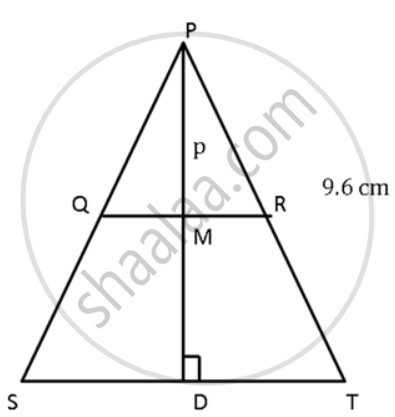
Since QR is parallel to ST
By Basic Theorem of Proportionality,
`"PQ"/"PS" = "PR"/"PT"`
⇒ `(3)/(4) = "PR"/(9.6)`
⇒ PR = `(9.6 xx 3)/(4)` = 7.2cm
Since QR is parallel to ST,
QM || SD
By Basic Theorem of Proportionality,
`"PQ"/"PS" = "PM"/"PD"`
⇒ `(3)/(4) = "P"/"PD"`
⇒ PD = `(4"p")/(3)`
So, the length of the perpendicular from P and ST in terms of p is `(4"p")/(3)`.
APPEARS IN
संबंधित प्रश्न
Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
In the given figure, QR is parallel to AB and DR is parallel to AB and DR is parallel to QB.

Prove that: PQ2 = PD × PA.
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In the given figure, DB⊥BC, DE⊥AB and AC⊥BC.
Prove that `(BE)/(DE)=(AC)/(BC)`

ΔABC ~ ΔDEF and their areas are respectively `100cm^2` and `49cm2`. If the altitude of ΔABC is 5cm, find the corresponding altitude of ΔDEF.
Select the appropriate alternative.
In ∆ABC and ∆PQR, in a one to one correspondence \[\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}\]

In figure, PQ is parallel to BC, AP : AB = 2 : 7. If QC = 0 and BC = 21,
Find
(i) AQ
(ii) PQ
A map is drawn to scale of 1:20000. Find: The distance on the map representing 4km
ABCD is a parallelogram. Point P divides AB in the ratio 2:3 and point Q divides DC in the ratio 4:1. Prove that OC is half of OA.

In figure, if AD = 6cm, DB = 9cm, AE = 8cm and EC = 12cm and ∠ADE = 48°. Find ∠ABC.

