Advertisements
Advertisements
Question
The sides PQ and PR of the ΔPQR are produced to S and T respectively. ST is drawn parallel to QR and PQ: PS = 3:4. If PT = 9.6 cm, find PR. If 'p' be the length of the perpendicular from P to QR, find the length of the perpendicular from P to ST in terms of 'p'.
Solution
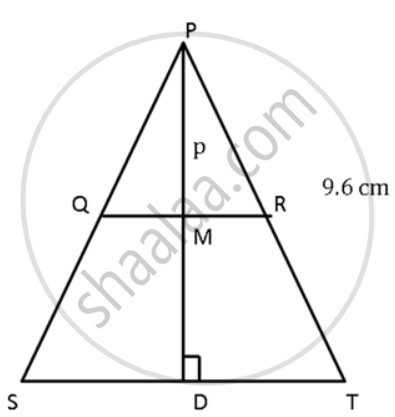
Since QR is parallel to ST
By Basic Theorem of Proportionality,
`"PQ"/"PS" = "PR"/"PT"`
⇒ `(3)/(4) = "PR"/(9.6)`
⇒ PR = `(9.6 xx 3)/(4)` = 7.2cm
Since QR is parallel to ST,
QM || SD
By Basic Theorem of Proportionality,
`"PQ"/"PS" = "PM"/"PD"`
⇒ `(3)/(4) = "P"/"PD"`
⇒ PD = `(4"p")/(3)`
So, the length of the perpendicular from P and ST in terms of p is `(4"p")/(3)`.
APPEARS IN
RELATED QUESTIONS
A vertical stick 20 cm long casts a shadow 6 cm long on the ground. At the same time, a tower casts a shadow 15 m long on the ground. Find the height of the tower.
P and Q are points on the sides AB and AC respectively of a ΔABC. If AP = 2cm, PB = 4cm, AQ = 3cm and QC = 6cm, show that BC = 3PQ.
In the given figure, seg XY || seg BC, then which of the following statements is true?

ABCD and PQRS are similar figures. AB= 12cm, BC=x cm, CD= 15 cm, AD= 10 cm, PQ= 8 cm, QR = 5 cm, RS = m cm and PS = n cm .Find the values of x, m and n.
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AD)/(AB)`

Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The area of land represented on the map.
If BD ⊥ AC and CE ⊥ AB, prove that `"CA"/"AB" = "CE"/"DB"`

