Advertisements
Advertisements
Question
In the given figure, seg XY || seg BC, then which of the following statements is true?

Options
`"AB"/"AC" = "AX"/"AY"`
`"AX"/"XB" ="AY"/"AC"`
`"AX"/"YC" = "AY"/"XB"`
`"AB"/"YC" = "AC"/"XB"`
Solution
Given: seg XY || seg BC
`"AX"/"BX" = "AY"/"YC"` .......(By basic proportionality theorem)
⇒ `("BX"/"AX") + 1 = ("YC"/"AY") + 1`
⇒ `("BX" + "AX")/"AX" = ("YC" + "AY")/"AY"`
⇒ `"AB"/"AX" = "AC"/"AY"`
⇒ `"AB"/"AC" = "AX"/"AY"`
Hence, the correct option is `"AB"/"AC" = "AX"/"AY"`
RELATED QUESTIONS
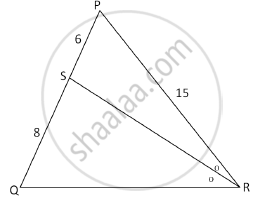
In the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 6, SQ = 8, PR = 15, find QR.
In the following figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

The two similar triangles are equal in area. Prove that the triangles are congruent.
The corresponding altitudes of two similar triangles are 6cm and 9cm respectively. Find the ratio of their areas.
In the given figure, DE║BC. If DE = 3cm, BC = 6cm and ar(ΔADE) = `15cm^2`, find the area of ΔABC.

In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and AC is 14 cm. If arcs of equal radii 7 cm taking A, B, C and D as centres, have been drawn, then find the area of the shaded region ?

As shown in figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m then how long will be the shadow of the bigger pole at the same time?

ΔABC ∼ ΔDEF and A(ΔABC) : A Δ(DEF) = 1 : 2 If AB = 4 find DE.
In Δ ABC, DE || BC; DC and EB intersects at F. if `"DE"/"BC" = 2/7` , find `("Ar" (triangle "FDE"))/("Ar" (triangle "FBC"))`
A triangle LMN has been reduced by scale factor 0.8 to the triangle L' M' N'. Calculate: the length of M' N', if MN = 8 cm.
Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AE"/"AC"`
In the figure, PR || SQ. If PR = 10cm, PT = 5cm, TQ = 6cm and ST = 9cm, calculate RT and SQ.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 8cm, Actual length = 20cm.
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆RPN

If BD ⊥ AC and CE ⊥ AB, prove that ∆AEC ~ ∆ADB

A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
In ΔDEF and ΔXYZ, `"DE"/"XY" = "FE"/"YZ"` and ∠E ≅ ∠Y. _______ test gives similarity between ΔDEF and ΔXYZ.

In the figure PQ || BC. If `"PQ"/"BC" = 2/5` then `"AP"/"PB"` is ______.

In figure, if AD = 6cm, DB = 9cm, AE = 8cm and EC = 12cm and ∠ADE = 48°. Find ∠ABC.

