Advertisements
Advertisements
Question
In the following figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

Solution
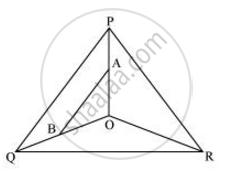
In Δ POQ, AB || PQ
∴ `("OA")/("AP") = ("OB")/("BQ")` ...(basic proportionality theorem) ...(i)
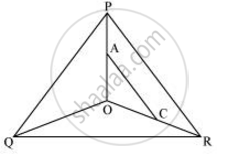
In ∆OPR, AC || PR
∴ `("OA")/("AP") = ("OC")/("CR")` ...(By basic proportionality theorem) ...(ii)
From (i) and (ii), we obtain
`("OB")/("BQ") = ("OC")/("CR")`
∴ `"BC" || "OQ"` ...(By Converse of basic proportionality theorem)
RELATED QUESTIONS
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 3, SQ = 9, PR = 18. Find QR.

In figure, QA and PB are perpendicular to AB. If AO = 10 cm, BO = 6 cm and PB = 9 cm. Find AQ
The perimeters of two similar triangles ABC and PQR are respectively 36 cm and 24 cm. If PQ = 10 cm, find AB
In figure, if ∠A = ∠C, then prove that ∆AOB ~ ∆COD

P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm, PB = 6cm. AQ = 5 cm and QC = 10 cm, show that BC = 3PQ.
Using Basic proportionality theorem, prove that a line drawn through the mid-points of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
Using Converse of basic proportionality theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that `("AO")/("BO") = ("CO")/("DO")`
Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles
`triangleDEF ~ triangleMNK`. If DE = 5 and MN = 6, then find the value of `(A(triangleDEF))/(A(triangleMNK))`
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

- ΔADE ∼ ΔACB.
- If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
- Find, area of ΔADE : area of quadrilateral BCED.
In the given figure ΔABC and ΔAMP are right angled at B and M respectively. Given AC = 10 cm, AP = 15 cm and PM = 12 cm.

1) Prove ΔABC ~ ΔAMP
2) Find AB and BC.
In the adjoining figure, ABC is a right angled triangle with ∠BAC = 90°.
1) Prove ΔADB ~ ΔCDA.
2) If BD = 18 cm CD = 8 cm Find AD.
3) Find the ratio of the area of ΔADB is to an area of ΔCDA.

Area of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5,

Find:
- ∆APB : ∆CPB
- ∆DPC : ∆APB
- ∆ADP : ∆APB
- ∆APB : ∆ADB
A model of a ship if made to a scale of 1 : 200.
(i) Thelength of the model is 4 m; calculate the length of the ship.
(ii) The area of the deck of the ship is 160000 m2; find the area of the deck of the model.
(iii) The volume of the model is 200 litres; calculate the volume of the ship in m3.
In the given figure, ΔOAB ~ ΔOCD. If AB = 8cm, BO = 6.4cm, OC = 3.5cm and CD = 5cm, find (i) OA (ii) DO.
The corresponding sides of two similar triangles ABC and DEF are BC = 9.1cm and EF = 6.5cm. If the perimeter of ΔDEF is 25cm, find the perimeter of ΔABC.
In the given figure, ∠ABC = 90° and BD⊥AC. If BD = 8cm, AD = 4cm, find CD.
ΔABC~ΔDEF and their areas are respectively 64 cm2 and 121cm2. If EF = 15.4cm, find BC.
The areas of two similar triangles are 169cm2 and 121cm2 respectively. If the longest side of the larger triangle is 26cm, find the longest side of the smaller triangle.
In ΔABC, D and E are the midpoints of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.

State the AA-similarity criterion
In the given figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF.

Proof : In ΔXDE, PQ || DE ...`square`
∴ `"XP"/square = square/"QE"` ...(I) (Basic proportionality theorem)
In ΔXEF, QR || EF ...`square`
∴ `square/square = square/square ..."(II)" square`
∴ `square/square = square/square` ...from (I) and (II)
∴ seg PR || seg DF ...(converse of basic proportionality theorem)
Are the triangles in the given figure similar? If yes, by which test?

In ∆ABC, AP ⊥ BC, BQ ⊥ AC B– P–C, A–Q – C then prove that, ∆CPA ~ ∆CQB. If AP = 7, BQ = 8, BC = 12 then Find AC.

If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E then which of the following statements is false?

Δ ABC ∼ Δ PQR. AD and PS are altitudes from A and P on sides BC and QR respectively. If AD : PS = 4 : 9 , find the ratio of the areas of Δ ABC and Δ PQR.
D and E are points on the sides AB and AC respectively of Δ ABC such that AB=5.6cm, AD= 1.4cm, AC=7 .2cm and AE = 1.5 cm, show that DE is parallel to BC
The length of a river in a map is 54cm. if lcm on the map represents 12500m on land, find the length of the river.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The area in km2 that can be represented by 1 cm2
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 11, SQ = 12, PR = 22. Find QR.

In the following figure, point D divides AB in the ratio 3 : 5. Find :
- `(AE)/(EC)`
- `(AD)/(AB)`
- `(AE)/(AC)`
Also, if: - DE = 2.4 cm, find the length of BC.
- BC = 4.8 cm, find the length of DE.

In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.

In the following figure, M is mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that : PE = 2 PD

Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
On a map drawn to scale of 1 : 2,50,000 a rectangular plot of land ABCD has the following measurement AB = 12 cm, BC = 16 cm angles A, B, C, and D are 900 each. Calculate:
(i) The diagonal distance of the plot of land in
(ii) Actual length of diagonal.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3,Find x.
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AD"/"AB"`
In ΔABC, point D divides AB in the ratio 5:7, Find: BC, If DE = 2.5cm
The sides PQ and PR of the ΔPQR are produced to S and T respectively. ST is drawn parallel to QR and PQ: PS = 3:4. If PT = 9.6 cm, find PR. If 'p' be the length of the perpendicular from P to QR, find the length of the perpendicular from P to ST in terms of 'p'.
Given that ΔABC ∼ ΔPRQ, name the corresponding angles and the corresponding sides.
Harmeet is 6 feet tall and casts a shadow of 3 feet long. What is the height of a nearby pole if it casts a shadow of 12 feet long at the same time?
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: Area of quadrilateral PBCQ: area of ΔABC.
Find the scale factor in each of the following and state the type of size transformation:
Actual length = 12cm, Image length = 15cm.
Find the scale factor in each of the following and state the type of size transformation:
Actual area = 64m2, Model area = 100cm2
A map is drawn to scale of 1:20000. Find: The distance on the map representing 4km
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN

If figure OPRQ is a square and ∠MLN = 90°. Prove that QR2 = MQ × RN

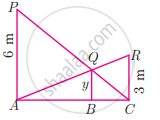
Two vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y
In ∆LMN, ∠L = 60°, ∠M = 50°. If ∆LMN ~ ∆PQR then the value of ∠R is
If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is
PR = 26 cm, QR = 24 cm, ∠PAQ = 90°, PA = 6 cm and QA = 8 cm. Find ∠PQR
A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
If ΔABC ~ ΔLMN and ∠A = 60° then ∠L = ?
State whether the following triangles are similar or not: If yes, then write the test of similarity.
∠P = 35°, ∠X = 35° and ∠Q = 60°, ∠Y = 60°

Two triangles are similar. Smaller triangle’s sides are 4 cm, 5 cm, 6 cm. Perimeter of larger triangle is 90 cm then find the sides of larger triangle.
In the figure PQ || BC. If `"PQ"/"BC" = 2/5` then `"AP"/"PB"` is ______.

In the given figure, ΔABC ∼ ΔQPR, If AC = 6 cm, BC = 5 cm, QR = 3 cm and PR = x; them the value of x is ______.

In the adjoining diagram the length of PR is ______.

