Advertisements
Advertisements
Question
Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles
Solution
In ΔABC, the coordinates of the vertices are A(–2, 0), B(2, 0), C(0, 2).
`AB = sqrt((2+2)^2 + (0 - 0)^2) = 4`
`BC = sqrt((0 - 2)^2 + (2 - 0)^2) =sqrt8 = 2sqrt2`
`CA = sqrt((0 + 2)^2 + (2 - 0)^2) = sqrt8 = 2sqrt2)`
In ΔPQR, the coordinates of the vertices are P(–4, 0), Q(4, 0), R(0, 4).
`PQ = sqrt((4+4)^2 + (0-0)^2) = 8`
`QR = sqrt((0 - 4)^2 + (4 - 0)^2) = 4sqrt2`
`PR= sqrt((0 + 4)^2 + (4 - 0)^2) = 4sqrt2`
Now, for ΔABC and ΔPQR to be similar, the corresponding sides should be proportional
So, `(AB)/(PQ) = (BC)/(QR) = (CA)/(PR)`
`=> 4/8 = (2sqrt2)/(4sqrt2) = (2sqrt2)/(4sqrt2) = 1/2`
Thus, ΔABC is similar to ΔPQR
APPEARS IN
RELATED QUESTIONS
Prove that the angle bisector of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
In a triangle ABC, line l || Side BC and line l intersects side AB and AC in points P and Q, respectively. Prove that: `"AP"/"BP"="AQ"/"QC"`

The diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC. Prove that DF × EF = FB × FA
In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
- Prove that ΔACD is similar to ΔBCA.
- Find BC and CD.
- Find area of ΔACD : area of ΔABC.

In ΔABC and ΔDEF, it is being given that: AB = 5 cm, BC = 4 cm and CA = 4.2 cm; DE=10cm, EF = 8 cm and FD = 8.4 cm. If AL ⊥ BC and DM ⊥ EF, find AL: DM.
E and F are the points in sides DC and AB respectively of parallelogram ABCD. If diagonal AC
and segment EF intersect at G; prove that:
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

The areas of two similar triangles are `81cm^2` and `49cm^2` respectively. If the altitude of the first triangle is 6.3cm, find the corresponding altitude of the other.
In ∆ABC, AP ⊥ BC, BQ ⊥ AC B– P–C, A–Q – C then prove that, ∆CPA ~ ∆CQB. If AP = 7, BQ = 8, BC = 12 then Find AC.

In ΔPQR, PQ = 10 cm, QR = 12cm, PR = 8 cm, find the biggest and the smallest angle of the triangle.
In Δ PQR, MN is drawn parallel to QR. If PM = x, MQ = (x-2), PN = (x+2) and NR = (x-1), find the value of x.
A model of a ship is made with a scale factor of 1 : 500. Find
The length of the ship, if the model length is 60 cm.
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of C' A' if CA = 4 cm.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OC', if OC = 21 cm.
Also, state the value of :
- `(OB^')/(OB)`
- `(C^'A^')/(CA)`
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.

Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
In the adjoining figure, the medians BD and CE of a ∆ABC meet at G. Prove that
(i) ∆EGD ∼ ∆CGB and
(ii) BG = 2GD for (i) above.
In ΔABC, MN is drawn parallel to BC. If AB = 3.5cm, AM : AB = 5 : 7 and NC = 2cm, find:
(i) AM
(ii) AC
ΔABC is right angled at A. AD is drawn perpendicular to BC. If AB = 8cm and AC = 6cm, calculate BD.
In the figure, PQR is a straight line and PS || RT. If QS = 12cm, QR = 15cm, QT = 10cm and RT = 6cm, find PQ and PS.
In a quadrilateral PQRS, the diagonals PR and QS intersect each other at the point T. If PT:TR = QT :TS = 1:2, show that ΔPTQ - DRTS
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate:Length of B' C', if BC = 8cm
A model of a ship is made to a scale of 1:500. Find: The volume of the model when the volume of the ship is 1km3
On a map drawn to a scale of 1:25000, a triangular plot of land is right angled and the sides forming the right angle measure 225cm and 64cm.Find: The area of the plot in sq. km.
Check whether the triangles are similar and find the value of x
Two vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y
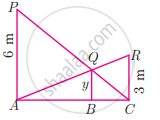
Write the test of similarity for triangles given in figure.
Is the following statement true? Why? “Two quadrilaterals are similar, if their corresponding angles are equal”.
