Advertisements
Advertisements
Question
The areas of two similar triangles are `81cm^2` and `49cm^2` respectively. If the altitude of the first triangle is 6.3cm, find the corresponding altitude of the other.
Solution
It is given that the triangles are similar.
Therefore, the areas of these triangles will be equal to the ratio of squares of their corresponding sides.
Also, the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
Let the two triangles be ABC and DEF with altitudes AP and DQ, respectively.
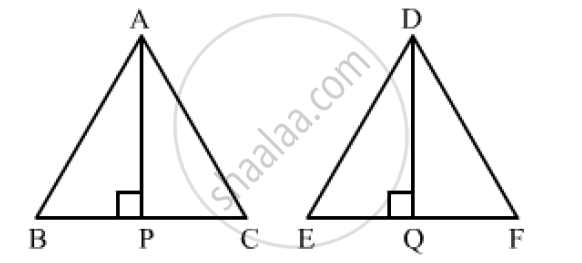`(ar(ΔABC))/(ar(ΔPQR))=(AP^2)/(DQ^2)`
⇒`81/49=6.3^2/(DQ^2)`
⇒ `DQ^2=49/81xx6.3^2`
⇒ `DQ^2=sqrt(49/81xx6.3xx6.3)`
Hence, the altitude of the other triangle is 4.9 cm
APPEARS IN
RELATED QUESTIONS
In the figure given below, Ray PT is bisector of ∠QPR. If PQ = 5.6 cm, QT = 4 cm and TR = 5 cm, find the value of x .
Given `triangle ABC ~ triangle PQR`, if `(AB)/(PQ) = 1/3`, then find `(ar triangle ABC)/(ar triangle PQR)`
In the given figure, AB and DE are perpendicular to BC.
1) Prove that ΔABC ∼ ΔDEC
2) If AB = 6 cm; DE = 4 cm and AC = 15 cm. Calculate CD.
3) Find the ratio of area of ΔABC: area of ΔDEC
In the given figure ABC is a triangle with ∠EDB = ∠ACB. Prove that Δ ABC ~ Δ EBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm. And area of Δ BED = 9 cm2. Calculate the
(1) length of AB
(2) area of Δ ABC
The perimeter of two similar triangles are 30 cm and 24 cm. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
In the given figure, BC is parallel to DE. Area of triangle ABC = 25 cm2, Area of trapezium BCED = 24 cm2 and DE = 14 cm. Calculate the length of BC. Also, find the area of triangle BCD.
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB) = 3/2`.
- Determine the ratios `(AD)/(AB)` and `(DE)/(BC)`.
- Prove that ∆DEF is similar to ∆CBF. Hence, find `(EF)/(FB).`
- What is the ratio of the areas of ∆DEF and ∆BFC?
The two similar triangles are equal in area. Prove that the triangles are congruent.
The given figure shows a triangle PQR in which XY is parallel to QR. If PX : XQ = 1 : 3 and QR = 9 cm, find the length of XY.
Further, if the area of ΔPXY = x cm2; find, in terms of x the area of :
- triangle PQR.
- trapezium XQRY.
In the given figure, if ∠ADE = ∠B, show that ΔADE ~ ΔABC. If AD = 3.8cm, AE = 3.6cm, BE = 2.1cm and BC = 4.2cm, find DE.
ABCD is parallelogram and E is a point on BC. If the diagonal BD intersects AE at F, prove that AF × FB = EF × FD.
In a circle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a) ΔPAC ∼PDB (b) PA. PB= PC.PD
Two chords AB and CD of a circle intersect at a point P outside the circle.
Prove that: (i) Δ PAC ~ Δ PDB (ii) PA. PB = PC.PD
The corresponding altitudes of two similar triangles are 6cm and 9cm respectively. Find the ratio of their areas.
In ΔABC, D and E are the midpoints of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
In Δ ABC, DE || BC; DC and EB intersects at F. if `"DE"/"BC" = 2/7` , find `("Ar" (triangle "FDE"))/("Ar" (triangle "FBC"))`
Figure shows Δ KLM , P an T on KL and KM respectively such that∠ KLM =∠ KTP.
If `"KL"/"KT" = 9/5` , find `("Ar" triangle "KLM")/("Ar" triangle "KTP")`.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in cm, of the model; if the length of the aeroplane is 40 m.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and ∠ABC = 90°.
Calculate : the actual lengths of AB and BC in km.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
DE = 2.4 cm, find the length of BC.
If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AD = 5.7cm, BD = 9.5cm, AE = 3.3cm, and EC = 5.5cm
Two figures are similar. If the ratio of their perimeters is 8:16. What will be the ratio of the corresponding sides?
In the adjacent figure, ∆ACB ~ ∆APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN
Construct a triangle similar to a given triangle PQR with its sides equal to `7/3` of the corresponding sides of the triangle PQR (scale factor `7/3 > 1`)
If BD ⊥ AC and CE ⊥ AB, prove that `"CA"/"AB" = "CE"/"DB"`
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that c2 = `"p"^2 - "a"x + "a"^2/4`
In the given figure YH || TE. Prove that ΔWHY ~ ΔWET and also find HE and TE
In the figure PQ || BC. If `"PQ"/"BC" = 2/5` then `"AP"/"PB"` is ______.
