Advertisements
Advertisements
Question
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB) = 3/2`.
- Determine the ratios `(AD)/(AB)` and `(DE)/(BC)`.
- Prove that ∆DEF is similar to ∆CBF. Hence, find `(EF)/(FB).`
- What is the ratio of the areas of ∆DEF and ∆BFC?
Solution
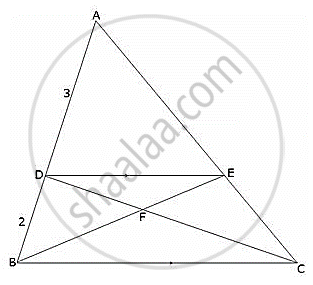
i. Given, DE || BC and `(AD)/(DB) = 3/2`
In ΔADE and ΔABC,
∠A = ∠A ...(Corresponding Angles)
∠ADE = ∠ABC ...(Corresponding Angles)
∴ ΔADE ∼ ΔABC ...(By AA- similarity)
`(AD)/(AB) = (AE)/(AC) = (DE)/(BC)` ...(1)
Now, `(AD)/(AB) = (AD)/(AD + DB) = 3/(3 + 2) = 3/5`
Using (1), we get `(AD)/(AE) = 3/5 = (DE)/(BC)` ...(2)
ii. In ∆DEF and ∆CBF,
∠FDE =∠FCB ...(Alternate Angle)
∠DFE = ∠BFC ...(Vertically Opposite Angle)
∴ ∆DEF ∼ ∆CBF ...(By AA- similarity)
`(EF)/(FB) = (DE)/(BC) = 3/5` Using (2)
`(EF)/(FB) = 3/5`
iii. Since the ratio of the areas of two similar triangles is equal to the square of the ratio of the corresponding sides, therefore.
`"Area of ΔDFE"/"Area of ΔCBF" = (EF^2)/(FB^2) = 3^2/5^2 = 9/25`
APPEARS IN
RELATED QUESTIONS
In an isosceles ΔABC, the base AB is produced both ways in P and Q such that
AP × BQ = AC2.
Prove that ΔACP~ΔBCQ.

In the following figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and \[\text{AD} = 9 \text{ find} \frac{A\left( \Delta ABE \right)}{A\left( \Delta BAD \right)} \cdot\]

In ∆ABC, ray BD bisects ∠ABC and ray CE bisects ∠ACB. If seg AB ≅ seg AC then prove that ED || BC.
In the figure, parts of the two triangles bearing identical marks are
congruent. State the test by which the triangles are congruent.

D and E are points on the sides AB and AC respectively of a Δ ABC such that DE | | BC and divides Δ ABC into two parts, equal in area. Find `"BD"/"AB"`.
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AE"/"AC"`
In a right-angled triangle ABC, ∠B = 90°, P and Q are the points on the sides AB and AC such as PQBC, AB = 8 cm, AQ = 6 cm and PA:AB = 1:3. Find the lengths of AC and BC.
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The base area of the truck, if the base area of the model is 30m2
PR = 26 cm, QR = 24 cm, ∠PAQ = 90°, PA = 6 cm and QA = 8 cm. Find ∠PQR
In Quadrilateral ABCD, side AD || BC, diagonal AC and BD intersect in point P, then prove that `"AP"/"PD" = "PC"/"BP"`
