Advertisements
Advertisements
Question
In a right-angled triangle ABC, ∠B = 90°, P and Q are the points on the sides AB and AC such as PQBC, AB = 8 cm, AQ = 6 cm and PA:AB = 1:3. Find the lengths of AC and BC.
Solution
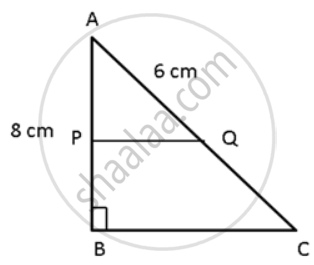
In right-angled ΔABC,
PQ || BC
⇒ `"PA"/"AB" = "QA"/"AC"`
⇒ `(1)/(3) = (6)/"AC"`
⇒ AC = 18cm
By Pythagoras Theorem,
BC2 = AC2 - AB2
⇒ BC2 = 182 - 82
⇒ BC2 = 324 - 64
⇒ BC = 16.12cm.
APPEARS IN
RELATED QUESTIONS
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In a right triangle ABC, right angled at B, D is a point on hypotenuse such that BD ⊥ AC , if DP ⊥ AB and DQ ⊥ BC then prove that
`(a) DQ^2 Dp.QC (b) DP ^2 DQ.AP 2 `

If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E then which of the following statements is false?


O is any point in the interior of ΔABC. Bisectors of ∠AOB, ∠BOC and ∠AOC intersect side AB, side BC, side AC in
F, D and E respectively.
Prove that
BF × AE × CD = AF × CE × BD
AD and BC are two straight lines intersecting at 0. CD and BA are perpendirulars from Band Con AD. If AB=6cm, CD =9cm, AD =20cm and BC=25cm, find the lengths of AO, BO, CO and DO.
Harmeet is 6 feet tall and casts a shadow of 3 feet long. What is the height of a nearby pole if it casts a shadow of 12 feet long at the same time?
Check whether the triangles are similar and find the value of x
If ∆ABC ~ ∆DEF such that area of ∆ABC is 9 cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
ΔPQR ~ ΔSUV. Write pairs of congruent angles
Prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
Using the above theorem prove that a line through the point of intersection of the diagonals and parallel to the base of the trapezium divides the non-parallel sides in the same ratio.
