Advertisements
Advertisements
प्रश्न
In a right-angled triangle ABC, ∠B = 90°, P and Q are the points on the sides AB and AC such as PQBC, AB = 8 cm, AQ = 6 cm and PA:AB = 1:3. Find the lengths of AC and BC.
उत्तर
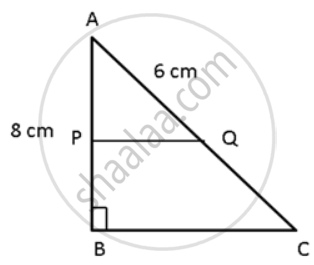
In right-angled ΔABC,
PQ || BC
⇒ `"PA"/"AB" = "QA"/"AC"`
⇒ `(1)/(3) = (6)/"AC"`
⇒ AC = 18cm
By Pythagoras Theorem,
BC2 = AC2 - AB2
⇒ BC2 = 182 - 82
⇒ BC2 = 324 - 64
⇒ BC = 16.12cm.
APPEARS IN
संबंधित प्रश्न
In the following figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

The diagonals of a quadrilateral ABCD intersect each other at the point O such that `("AO")/("BO") = ("CO")/("DO")`. Show that ABCD is a trapezium.
In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that:

- ΔEGD ~ ΔCGB and
- BG = 2GD from (i) above.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The area in km2 that can be represented by 1 cm2
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find
The area on the map that represents the plot of land.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OA, if OA' = 6 cm.
A line PQ is drawn parallel to the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP.
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AD"/"AB"`
In ΔABC, DE is drawn parallel to BC cutting AB in the ratio 2 : 3. Calculate:
(i) `("area"(Δ"ADE"))/("area"(Δ"ABC")`
(i) `("area"("trapeziumEDBC"))/("area"(Δ"ABC"))`
An architecture have model of building. Length of building is 1 m then length of model is 0.75 cm. Then find length and height of model building whose actual length is 22.5 m and height is 10 m
