Advertisements
Advertisements
Question

O is any point in the interior of ΔABC. Bisectors of ∠AOB, ∠BOC and ∠AOC intersect side AB, side BC, side AC in
F, D and E respectively.
Prove that
BF × AE × CD = AF × CE × BD
Solution
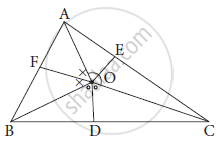
In Δ AOB, OF is bisector of ∠ AOB
∴`(OA)/(OB) = (AF)/(BF)` ....... (1) (by angle bisector theoerm)
In Δ BOC, OD is bisector of angle ∠ BOC .
∴`(OB)/(OC) =( BD)/(CD)` ....... (2)(by angle bisector theoerm)
In Δ AOC , OE is bisector of angle∠ AOC.
∴`( OC)/(OA) = (CE)/(AE)` ....... (3)(by angle bisector theoerm)
∴ `(OA)/(OB) ×( OB)/(OC) × (OC)/(OA) = (AF)/(BF) ×( BD)/(CD) × (CE)/(AE)` from (1), (2) and (3)
`therefore(OAxxOCxxOB)/(OBxxOAxxOC) = (AFxxBFxxCE)/(BDxxAExxCD)`
` therefore1 = (AFxxCExxBD)/(BFxxAExxCD)`
∴ BF × AE × CD = AF × CE × BD
APPEARS IN
RELATED QUESTIONS
In figure, if ∠A = ∠C, then prove that ∆AOB ~ ∆COD

In the given figure, AB and DE are perpendicular to BC.

1) Prove that ΔABC ∼ ΔDEC
2) If AB = 6 cm; DE = 4 cm and AC = 15 cm. Calculate CD.
3) Find the ratio of area of ΔABC: area of ΔDEC
On a map, drawn to a scale of 1 : 250000, a triangular plot PQR of land has the following measurements :
PQ = 3cm, QR = 4 cm and angles PQR = 90°
(i) the actual lengths of QR and PR in kilometer.
(ii) the actual area of the plot in sq . km.
ΔABC ~ ΔDEF and their areas are respectively `100cm^2` and `49cm2`. If the altitude of ΔABC is 5cm, find the corresponding altitude of ΔDEF.
State the SSS-similarity criterion for similarity of triangles
Select the appropriate alternative.
In ∆ABC and ∆PQR, in a one to one correspondence \[\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}\]

A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OA, if OA' = 6 cm.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
Let ∆ ABC ∽ ∆ DEF and their areas be respectively, 64 cm2 and 121 cm2. If EF = 15⋅4 cm, find BC.
Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
In the given figure ABC and CEF are two triangles where BA is parallel to CE and AF: AC = 5: 8.
(i) Prove that ΔADF ∼ ΔCEF
(ii) Find AD if CE = 6 cm
(iii) If DF is parallel to BC find area of ΔADF: area of ΔABC.
The sides PQ and PR of the ΔPQR are produced to S and T respectively. ST is drawn parallel to QR and PQ: PS = 3:4. If PT = 9.6 cm, find PR. If 'p' be the length of the perpendicular from P to QR, find the length of the perpendicular from P to ST in terms of 'p'.
In ΔABC, DE is drawn parallel to BC cutting AB in the ratio 2 : 3. Calculate:
(i) `("area"(Δ"ADE"))/("area"(Δ"ABC")`
(i) `("area"("trapeziumEDBC"))/("area"(Δ"ABC"))`
ΔABC is enlarged, with a scale factor 5. Find: BC, f B'C' = 16cm
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The diagonal distance of the plot in km
If ΔABC ~ ΔLMN and ∠A = 60° then ∠L = ?
There are two poles having heights 8 m and 4 m on plane ground as shown in fig. Because of sunlight shadows of smaller pole is 6m long, then find the length of shadow of longer pole.
Side of equilateral triangle PQR is 8 cm then find the area of triangle whose side is half of the side of triangle PQR.
In the figure PQ || BC. If `"PQ"/"BC" = 2/5` then `"AP"/"PB"` is ______.

It is given that ΔABC ~ ΔPQR, with `(BC)/(QR) = 1/3`. Then, `(ar(PRQ))/(ar(BCA))` is equal to ______.
