Advertisements
Advertisements
प्रश्न

O is any point in the interior of ΔABC. Bisectors of ∠AOB, ∠BOC and ∠AOC intersect side AB, side BC, side AC in
F, D and E respectively.
Prove that
BF × AE × CD = AF × CE × BD
उत्तर
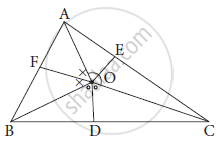
In Δ AOB, OF is bisector of ∠ AOB
∴`(OA)/(OB) = (AF)/(BF)` ....... (1) (by angle bisector theoerm)
In Δ BOC, OD is bisector of angle ∠ BOC .
∴`(OB)/(OC) =( BD)/(CD)` ....... (2)(by angle bisector theoerm)
In Δ AOC , OE is bisector of angle∠ AOC.
∴`( OC)/(OA) = (CE)/(AE)` ....... (3)(by angle bisector theoerm)
∴ `(OA)/(OB) ×( OB)/(OC) × (OC)/(OA) = (AF)/(BF) ×( BD)/(CD) × (CE)/(AE)` from (1), (2) and (3)
`therefore(OAxxOCxxOB)/(OBxxOAxxOC) = (AFxxBFxxCE)/(BDxxAExxCD)`
` therefore1 = (AFxxCExxBD)/(BFxxAExxCD)`
∴ BF × AE × CD = AF × CE × BD
APPEARS IN
संबंधित प्रश्न
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 3, SQ = 9, PR = 18. Find QR.

Prove that the angle bisector of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
In ΔPQR, MN is parallel to QR and `(PM)/(MQ) = 2/3`
1) Find `(MN)/(QR)`
2) Prove that ΔOMN and ΔORQ are similar.
3) Find, Area of ΔOMN : Area of ΔORQ

In the given figure, if ∠ADE = ∠B, show that ΔADE ~ ΔABC. If AD = 3.8cm, AE = 3.6cm, BE = 2.1cm and BC = 4.2cm, find DE.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
The dimensions of the model of a multistorey building are 1.2 m × 75 cm × 2 m. If the scale factor is 1 : 30; find the actual dimensions of the building.
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 11, SQ = 12, PR = 22. Find QR.

In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AD)/(AB)`

In the given figure, ΔABC ~ ΔADE. If AE : EC = 4 : 7 and DE = 6.6 cm, find BC. If 'x' be the length of the perpendicular from A to DE, find the length of perpendicular from A to BC in terms of 'x'.

In the figure, given below, PQR is a right-angle triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.

In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3,Find x.
ΔABC is right angled at A. AD is drawn perpendicular to BC. If AB = 8cm and AC = 6cm, calculate BD.
A map is drawn to scale of 1:20000. Find: The distance covered by 6cm on the map
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The diagonal distance of the plot in km
If ∆ABC ~ ∆DEF such that area of ∆ABC is 9 cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
If BD ⊥ AC and CE ⊥ AB, prove that ∆AEC ~ ∆ADB

In the given figure, if ΔEAT ~ ΔBUN, find the measure of all angles.
In Quadrilateral ABCD, side AD || BC, diagonal AC and BD intersect in point P, then prove that `"AP"/"PD" = "PC"/"BP"`
Areas of two similar triangles are equal then prove that triangles are congruent
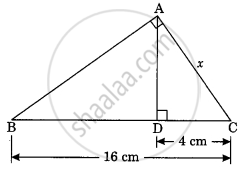
In the given figure the value of x is