Geometry Mathematics 2 Balbharati Model Question Paper Set 3 2018-2019 SSC (English Medium) 10th Standard Board Exam Question Paper Solution

The co-ordinates of point A and B are 4 and -8 respectively. Find d(A, B).

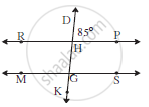
In the adjoining figure line RP ||line MS , line DK is a transversal . If ∠DHP = 85° find ∠RHG and ∠HGS.

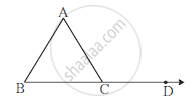
∠ACD is an exterior angle of Δ ABC. If ∠B = 40o, ∠A = 70o find ∠ACD.

Digonals of parallelogram WXYZ intersect at point O. If OY =5, find WY.

In which qudrant does point A(-3, 2) lie?
On which axis does point B(12, 0) lie?

Find the curved surface area of a sphere of radius 1cm. (π = 3.14)

Simplify : 2 sin30 + 3 tan45.

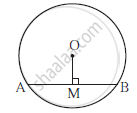
In the adjoining figure, point O is the centre of the cirlcle, seg OM ⊥ chord AB. If OM = 8cm, AB = 12 cm, then find OB.

In ΔPQR, PQ = 10 cm, QR = 12cm, PR = 8 cm, find the biggest and the smallest angle of the triangle.

How many common tangents can be drawn to two circles which touch each other internally?

(A) One (B) Two (C) Three (D) Four

Distance of point (-3, 4) from the origin is .....
(A) 7 (B) 1 (C) 5 (D) 4

Four alternative answers for the following question are given. Choose the correct alternative and write its alphabet:

sin θ × cosec θ = ______

1

0

`1/2`

`sqrt2`

Measure of an arc of a sector of a circle is 900 and its radius is 7cm. Find the perimeter of the sector.
(A) 44 cm (B) 25 cm (C) 36 cm (D) 56 cm

ΔABC ∼ ΔDEF and A(ΔABC) : A Δ(DEF) = 1 : 2 If AB = 4 find DE.

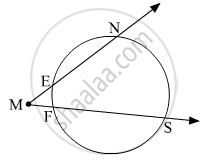
In the given figure, m(arc NS) = 125°, m(arc EF) = 37°, find the measure ∠NMS.

Find th co-ordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20).

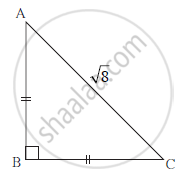
With the help of the information given in the figure, fill in the boxes to find AB and BC .

AB = BC                    (Given)

∴∠ BAC = ∠ BCA =     
∴ AB = BC =    × AC
=     × `sqrt8`
=        × `2sqrt2`
= 2

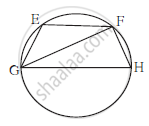
In the adjoining figure chord EF || chord GH.
Prove that chord EG ≅ chord FH.
Fill in the boxes and write the complete proof.

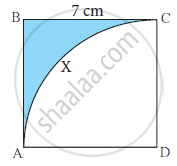
Side of square ABCD is 7 cm. With D as the centre and DA as radius, arc AXC is drawn.Find the area of the shaded region with the help of the following flow chart .

In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.

Prove that secθ + tanθ =`(costheta)/(1-sintheta)`.

Radii of the top and the base of a frustum of a cone are 5 cm and 2 cm respectively. Its height is 9 cm. Find its volume. (π = 3.14)

Prove that :
“If a line parallel to a side of a triangle intersects the remaining sides in two distince points, then the line divides the sides in the same proportion.”

Draw a circle with centre O and radius 3.5 cm. Take point P at a distance 5.7 cm from the centre. Draw tangents to the circle from point P.

Line PQ is parallel to line RS where points P,Q,R and S have
co-ordinates (2, 4), (3, 6), (3, 1) and (5, k) respectively. Find value of k.

From the top of a light house, an abserver looking at a boat makes an angle of depression of 600. If the height of the lighthouse is 90 m then find how far is the boat from the lighthouse. (3 = 1.73)

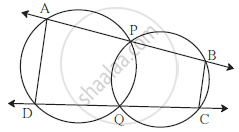
Two circles intersect each other at points P and Q. Secants drawn through P and Q intersect the circles at points A,B and D,C. Prove that : ∠ADC + ∠BCD = 180°

ΔXYZ ∼ ΔPYR; In ΔXYZ, ∠Y = 60o, XY = 4.5 cm, YZ = 5.1 cm and XYPY =` 4/7` Construct ΔXYZ and ΔPYR.

O is any point in the interior of ΔABC. Bisectors of ∠AOB, ∠BOC and ∠AOC intersect side AB, side BC, side AC in
F, D and E respectively.
Prove that
BF × AE × CD = AF × CE × BD

There is a hemispherical bowl. A cone is to be made such that, if it is filled with water twice and the water is poured in the bowl, it will be filled just completely. State how will you decide the radius and perpendicular height of the cone.