Advertisements
Advertisements
प्रश्न
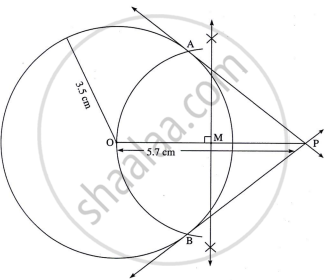
Draw a circle with centre O and radius 3.5 cm. Take point P at a distance 5.7 cm from the centre. Draw tangents to the circle from point P.
उत्तर
Steps of Construction:
Step 1: Construct a circle of radius 3.5 cm with centre O.
Step 2: Take a point P in the exterior of the circle such that OP = 5.7 cm
Step 3: Draw segment OP. Draw perpendicular bisector of segment OP to get its midpoint M.
Step 4: Draw a circle with radius OM and centre M.
Step 5: Name the point of intersection of the two circles as A and B.
Step 6: Draw line PA and line PB.
APPEARS IN
संबंधित प्रश्न
Draw a tangent at any point ‘P’ on the circle of radius 3.5 cm and centre O.
Draw a circle of radius 3.6 cm. Draw a tangent to the circle at any point on it without using the centre.
Draw a circle with radius 3.4 cm. Draw a chord MN of length 5.7 cm in it. construct tangents at point M and N to the circle.
Draw any circle. Take any point A on it and construct tangent at A without using the centre of the circle.
Complete the following activity to draw a tangent to a circle at a point on the circle.
Draw a circle of radius 2.2 cm with O as centre.
↓
Take any point P on the circle and draw ray OP.
↓
Draw a perpendicular line to the ray at point P.
↓
Name the perpendilcular line as l
l is the tangent at point P.
Choose the correct alternative:
______ number of tangents can be drawn to a circle from the point outside the circle
Draw a circle of radius 4.2 cm, take any point M on it. Draw tangent to the circle from point M
Draw a circle of radius 3.4 cm. Draw a chord MN 5.7 cm long in a circle. Draw a tangent to the circle from point M and point N
Complete the following activity to draw tangents to the circle.
- Draw a circle with radius 3.3 cm and center O. Draw chord PQ of length 6.6 cm. Draw ray OP and ray OQ.
- Draw a line perpendicular to the ray OP from P.
- Draw a line perpendicular to the ray OQ from Q.
Do the following activity to draw tangents to the circle without using the center of the circle.
- Draw a circle with radius 3.5 cm and take any point C on it.
- Draw chord CB and an inscribed angle CAB.
- With the center A and any convenient radius, draw an arc intersecting the sides of angle BAC in points M and N.
- Using the same radius, draw an arc intersecting the chord CB at point R.
- Taking the radius equal to d(MN) and center R, draw an arc intersecting the arc drawn in the previous step. Let D be the point of intersection of these arcs. Draw line CD. Line CD is the required tangent to the circle.
Draw a circle with center O and radius 3.4. Draw a chord MN of length 5.7 cm in a circle. Draw tangents to the circle from point M and N
Draw a circle with center O and radius 3.6 cm. Draw a tangent to the circle from point B at a distance of 7.2 cm from the center of the circle.
Draw a circle with center C and radius 3.2 cm. Draw a tangent to the circle from point P at a distance of 7.5 cm from the center of the circle
Draw a circle with a radius of 3.5 cm. Take the point K anywhere on the circle. Draw a tangent to the circle from K (without using the center of the circle)
Draw a circle of radius 4.2 cm. Draw arc PQ measuring 120°. Draw a tangent to the circle from point P and point Q
Take point P and Q and draw a circle passing through them. Draw a tangent AB to the circle without using the centre of the circle.
Draw any circle with radius greater than 1.8 cm and less than 3 cm. Draw a chord AB 3.6 cm long in this circle. Tangent to the circle passing through A and B without using the center of the circle
Draw a circle of radius 3.2 cm and centre 'O'. Take any point P on it. Draw tangent to the circle through point P using the centre of the circle.
Draw a circle of radius 4 cm. Draw a point 8 cm away from its centre and construct a pair of tangents.
