Advertisements
Advertisements
प्रश्न
ΔABC is right angled at A. AD is drawn perpendicular to BC. If AB = 8cm and AC = 6cm, calculate BD.
उत्तर
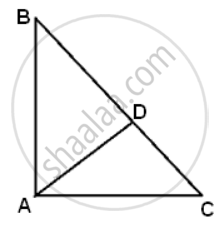
In ΔABC,
Using Pythagoras theorem
BC2 = AB2 + AC2
BC2 = 82 + 62
BC2 = 64 + 36
BC = `sqrt(100)` = 10..........(i)
In ΔABD,
Using Pythagoras theorem
AD2 = AB2 - BD2
AD2 = 82 - BD2......(ii)
In ΔACD,
Using Pythagoras theorem
AD2 = AC2 - CD2
AD2 = 62 - CD2......(iii)
Equaliting (ii) and (iii)
82 - BD2 = 62 - CD
∵ CD = BC - BD
82 - BD2 = 62 - (BC - BD)2
CD = BC - BD
BC = 10cm(from (i))
82 - BD2 = 62 - (10 - BD)2
82 - BD2 = 62 - (100 - 20BD + BD2)
64 + BD2 = 62 - (100 + 20BD - BD2)
64 = -64 + 20BD
20BD = 128
BD = 6.4cm.
APPEARS IN
संबंधित प्रश्न
In figure, ∠A = ∠CED, prove that ∆CAB ~ ∆CED. Also, find the value of x.

The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5,

Find:
- ∆APB : ∆CPB
- ∆DPC : ∆APB
- ∆ADP : ∆APB
- ∆APB : ∆ADB
State the SSS-similarity criterion for similarity of triangles
Δ ABC is similar to Δ PQR. If AB = 6cm, BC = 9cm, PQ = 9cm and PR = 10.5cm, find the lengths of AC and QR.
In Δ ABC, D and E are points on the sides AB and AC respectively. If AD= 4cm, DB=4.Scm, AE=6.4cm and EC=7.2cm, find if DE is parallel to BC or not.
The length of a river in a map is 54cm. if lcm on the map represents 12500m on land, find the length of the river.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4, AE = 8, DB = x - 4 and EC = 3x - 19, find x.
The dimensions of the model of a building are 1.2m x 75cm x 2m. If the scale factor is 1 : 20; find the actual dimensions of the building.
ΔDEF ~ ΔABC. If DE : AB = 2 : 3 and ar ΔDEF is equal to 44 square units then ar (ΔABC) (square unit) is ______.
In the given figure, ∠ACB = ∠CDA, AC = 8cm, AD = 3cm, then BD is ______.

