Advertisements
Advertisements
Question
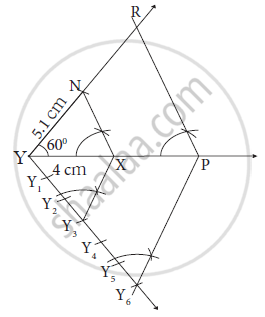
ΔXYZ ∼ ΔPYR; In ΔXYZ, ∠Y = 60o, XY = 4.5 cm, YZ = 5.1 cm and XYPY =` 4/7` Construct ΔXYZ and ΔPYR.
Solution
APPEARS IN
RELATED QUESTIONS
The coordinates of the point P are (−3, 2). Find the coordinates of the point Q which lies on the line joining P and origin such that OP = OQ.
Find the value of k, if the point P (0, 2) is equidistant from (3, k) and (k, 5).
In Fig. 14.36, a right triangle BOA is given C is the mid-point of the hypotenuse AB. Show that it is equidistant from the vertices O, A and B.

We have a right angled triangle,`triangle BOA` right angled at O. Co-ordinates are B (0,2b); A (2a, 0) and C (0, 0).
If the point P (2,2) is equidistant from the points A ( -2,K ) and B( -2K , -3) , find k. Also, find the length of AP.
The line segment joining A( 2,9) and B(6,3) is a diameter of a circle with center C. Find the coordinates of C
Write the coordinates the reflections of points (3, 5) in X and Y -axes.
If points Q and reflections of point P (−3, 4) in X and Y axes respectively, what is QR?
Find the area of triangle with vertices ( a, b+c) , (b, c+a) and (c, a+b).
The distance between the points (a cos θ + b sin θ, 0) and (0, a sin θ − b cos θ) is
The line segment joining points (−3, −4), and (1, −2) is divided by y-axis in the ratio.
If the centroid of the triangle formed by (7, x) (y, −6) and (9, 10) is at (6, 3), then (x, y) =
If P is a point on x-axis such that its distance from the origin is 3 units, then the coordinates of a point Q on OY such that OP = OQ, are
The coordinates of a point on x-axis which lies on the perpendicular bisector of the line segment joining the points (7, 6) and (−3, 4) are
The ratio in which the line segment joining points A (a1, b1) and B (a2, b2) is divided by y-axis is
If P(2, 4), Q(0, 3), R(3, 6) and S(5, y) are the vertices of a parallelogram PQRS, then the value of y is
If segment AB is parallel Y-axis and coordinates of A are (1, 3), then the coordinates of B are ______
Abscissa of all the points on the x-axis is ______.
Points (1, –1) and (–1, 1) lie in the same quadrant.
