Advertisements
Advertisements
प्रश्न
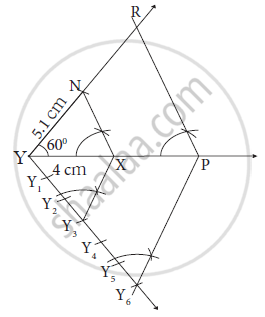
ΔXYZ ∼ ΔPYR; In ΔXYZ, ∠Y = 60o, XY = 4.5 cm, YZ = 5.1 cm and XYPY =` 4/7` Construct ΔXYZ and ΔPYR.
उत्तर
APPEARS IN
संबंधित प्रश्न
Find the distance between the following pair of points:
(a, 0) and (0, b)
Prove that the points (−2, 5), (0, 1) and (2, −3) are collinear.
Find the coordinates of the circumcentre of the triangle whose vertices are (3, 0), (-1, -6) and (4, -1). Also, find its circumradius.
Find a point on y-axis which is equidistant from the points (5, -2) and (-3, 2).
Find the ratio in which the point (2, y) divides the line segment joining the points A (-2,2) and B (3, 7). Also, find the value of y.
Prove that the points (4, 5) (7, 6), (6, 3) (3, 2) are the vertices of a parallelogram. Is it a rectangle.
Find the points on the x-axis, each of which is at a distance of 10 units from the point A(11, –8).
If the point ( x,y ) is equidistant form the points ( a+b,b-a ) and (a-b ,a+b ) , prove that bx = ay
Find the ratio in which the point (−3, k) divides the line-segment joining the points (−5, −4) and (−2, 3). Also find the value of k ?
The perpendicular distance of the P (4,3) from y-axis is
If the points A(−2, 1), B(a, b) and C(4, −1) ae collinear and a − b = 1, find the values of aand b.
If the distance between points (x, 0) and (0, 3) is 5, what are the values of x?
The area of the triangle formed by (a, b + c), (b, c + a) and (c, a + b)
The ratio in which the x-axis divides the segment joining (3, 6) and (12, −3) is
If the points(x, 4) lies on a circle whose centre is at the origin and radius is 5, then x =
If the centroid of the triangle formed by the points (3, −5), (−7, 4), (10, −k) is at the point (k −1), then k =
If P(2, 4), Q(0, 3), R(3, 6) and S(5, y) are the vertices of a parallelogram PQRS, then the value of y is
Find the point on the y-axis which is equidistant from the points (5, −2) and (−3, 2).
Assertion (A): The ratio in which the line segment joining (2, -3) and (5, 6) internally divided by x-axis is 1:2.
Reason (R): as formula for the internal division is `((mx_2 + nx_1)/(m + n) , (my_2 + ny_1)/(m + n))`
