Advertisements
Advertisements
Question
Side of equilateral triangle PQR is 8 cm then find the area of triangle whose side is half of the side of triangle PQR.
Solution
Given: ΔPQR is an equilateral triangle with PQ = QR = PR = 8 cm and ΔABC is an equilateral triangle with AB = BC = AC = 4 cm
To find: A(ΔABC)
Construction: Draw seg AD ⊥ BC, B−D−C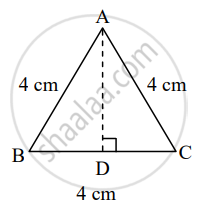
In ΔABD,
∠ADB = 90° ...[Construction]
∠ABD = 60° ...[Angle of an equilateral triangle]
∠BAD = 30° ...[Remaining angle of a triangle]
∴ ΔABD is a 30°–60°–90° triangle.
∴ AD = `sqrt(3)/2` AB ...[Side opposite to 60°]
∴ AD = `sqrt(3)/2 xx 4`
∴ AD = `2sqrt(3)` ...(i)
Area of triangle = `1/2 xx "height" xx "base" `
∴ Area of ΔABC = `1/2 xx "AD" xx "BC"`
= `1/2 xx 2sqrt(3) xx 4`
= `2 xx 2sqrt(3)`
= `4sqrt(3)` ......[From (i)]
∴ Area of the triangle whose side is half of the side of ΔPQR is `4sqrt(3)` sq.cm
APPEARS IN
RELATED QUESTIONS
In ΔPQR, MN is parallel to QR and `(PM)/(MQ) = 2/3`
1) Find `(MN)/(QR)`
2) Prove that ΔOMN and ΔORQ are similar.
3) Find, Area of ΔOMN : Area of ΔORQ

In the given figure ΔABC and ΔAMP are right angled at B and M respectively. Given AC = 10 cm, AP = 15 cm and PM = 12 cm.

1) Prove ΔABC ~ ΔAMP
2) Find AB and BC.
In the given figure, ∠CAB = 90° and AD⊥BC. Show that ΔBDA ~ ΔBAC. If AC = 75cm, AB = 1m and BC = 1.25m, find AD.

In Δ ABC, DE || BC; DC and EB intersects at F. if `"DE"/"BC" = 2/7` , find `("Ar" (triangle "FDE"))/("Ar" (triangle "FBC"))`
In Δ ABC, D and E are points on the sides AB and AC respectively. If AD= 4cm, DB=4.Scm, AE=6.4cm and EC=7.2cm, find if DE is parallel to BC or not.
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AD)/(AB)`

In the following figure, point D divides AB in the ratio 3 : 5. Find :
DE = 2.4 cm, find the length of BC.

In the following figure, point D divides AB in the ratio 3 : 5. Find :
BC = 4.8 cm, find the length of DE.

D and E are points on the sides AB and AC respectively of a Δ ABC such that DE | | BC and divides Δ ABC into two parts, equal in area. Find `"BD"/"AB"`.
In the given figure, AB and DE are perpendicular to BC.

- Prove that ΔABC ∼ ΔDEC
- If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
- Find the ratio of the area of a ΔABC : area of ΔDEC.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4, AE = 8, DB = x - 4 and EC = 3x - 19, find x.
If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AD = 5.7cm, BD = 9.5cm, AE = 3.3cm, and EC = 5.5cm
Find the scale factor in each of the following and state the type of size transformation:
Model area = 75cm2, Actual area = 3cm2
Find the scale factor in each of the following and state the type of size transformation:
Model volume = 200cm3, Actual volume = 8cm3
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is
ΔABC ~ ΔPQR, A(ΔABC) = 80 sq.cm, A(ΔPQR) = 125 sq.cm, then complete `("A"(Δ"ABC"))/("A"(Δ"PQR")) = 80/125 = (["______"])/(["______"])`, hence `"AB"/"PQ" = (["______"])/(["______"])`
In ∠BAC = 90° and AD ⊥ BC. A then ______.

In figure, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.
Prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
Using the above theorem prove that a line through the point of intersection of the diagonals and parallel to the base of the trapezium divides the non-parallel sides in the same ratio.
In figure, if AD = 6 cm, DB = 9 cm, AE = 8 cm and EC = 12 cm and ∠ADE = 48°. Find ∠ABC.

