Advertisements
Advertisements
प्रश्न
Side of equilateral triangle PQR is 8 cm then find the area of triangle whose side is half of the side of triangle PQR.
उत्तर
Given: ΔPQR is an equilateral triangle with PQ = QR = PR = 8 cm and ΔABC is an equilateral triangle with AB = BC = AC = 4 cm
To find: A(ΔABC)
Construction: Draw seg AD ⊥ BC, B−D−C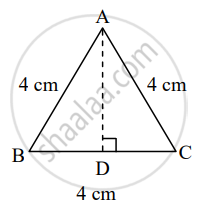
In ΔABD,
∠ADB = 90° ...[Construction]
∠ABD = 60° ...[Angle of an equilateral triangle]
∠BAD = 30° ...[Remaining angle of a triangle]
∴ ΔABD is a 30°–60°–90° triangle.
∴ AD = `sqrt(3)/2` AB ...[Side opposite to 60°]
∴ AD = `sqrt(3)/2 xx 4`
∴ AD = `2sqrt(3)` ...(i)
Area of triangle = `1/2 xx "height" xx "base" `
∴ Area of ΔABC = `1/2 xx "AD" xx "BC"`
= `1/2 xx 2sqrt(3) xx 4`
= `2 xx 2sqrt(3)`
= `4sqrt(3)` ......[From (i)]
∴ Area of the triangle whose side is half of the side of ΔPQR is `4sqrt(3)` sq.cm
APPEARS IN
संबंधित प्रश्न
In figure, ∆ACB ~ ∆APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm, AP = 2.8 cm, find CA and AQ.
In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
In the following figure, if LM || CB and LN || CD, prove that `("AM")/("AB")=("AN")/("AD")`

In the following figure, DE || OQ and DF || OR, show that EF || QR.

In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC ∼ ΔPDB
(ii) PA.PB = PC.PD

A model of a ship if made to a scale of 1 : 200.
(i) Thelength of the model is 4 m; calculate the length of the ship.
(ii) The area of the deck of the ship is 160000 m2; find the area of the deck of the model.
(iii) The volume of the model is 200 litres; calculate the volume of the ship in m3.
In the given triangle P, Q and R are the mid-points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In the given figure, DE║BC. If DE = 3cm, BC = 6cm and ar(ΔADE) = `15cm^2`, find the area of ΔABC.

In the following figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and \[\text{AD} = 9 \text{ find} \frac{A\left( \Delta ABE \right)}{A\left( \Delta BAD \right)} \cdot\]

On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and ∠ABC = 90°.
Calculate : the actual lengths of AB and BC in km.
In the given figure, ΔABC ~ ΔADE. If AE : EC = 4 : 7 and DE = 6.6 cm, find BC. If 'x' be the length of the perpendicular from A to DE, find the length of perpendicular from A to BC in terms of 'x'.

In the figure, given below, PQR is a right-angle triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.

Sides of a triangle are 7, 24 and 25. Determine whether the triangle is a right-angled triangle or not.
In ΔPQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP.
Prove that : (i) ΔPQL ∼ ΔRPM
(ii) QL. Rm = PL. PM
(iii) PQ2 = QR. QL.
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The area of land represented on the map.
If figure OPRQ is a square and ∠MLN = 90°. Prove that QR2 = MQ × RN

D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that c2 = `"p"^2 - "a"x + "a"^2/4`
∆ABC ~ ∆PQR. If AM and PN are altitudes of ΔABC and ∆PQR respectively and AB2 : PQ2 = 4 : 9, then AM : PN = ______.
